Em algumas situações a avaliação de incertezas pode ser feita na força bruta, simplesmente através da repetição de um experimento e avaliação dos desvios padrão da amostra obtida. Por exemplo, imagine-se jogando um balão de água do alto de uma torre. Você pode medir o tempo de queda deste balão e, através de um cálculo simples, supondo o movimento como sendo uniformemente variado e partindo do repouso, calcular a aceleração deste balão. Pois bem, para avaliar a incerteza nesta aceleração simplesmente repete-se à exaustão o experimento. Para cada balão jogado calcula-se a aceleração. No final, calcula-se a média das acelerações, desvio padrão e desvio padrão da média. Tem-se, portanto, o valor médio da aceleração e sua incerteza. O que aconteceu, de fato, é que a flutuação no tempo de queda do balão gerou uma flutuação na aceleração medida (veja a figura 1). Essas flutuações foram avaliadas simplesmente através da repetição da medida.

Figura 1 – Histograma com dados de um experimento de queda repetido 1500 vezes. A flutuação na medida de tempo gera uma flutuação no valor calculado de aceleração.
Por outro lado, em muitas situações não é possível repetir a medida à exaustão de forma a avaliar essas flutuações e o impacto delas em grandezas derivadas. Em uma situação bem simples, tem-se a medida  e quer-se calcular a grandeza
e quer-se calcular a grandeza  , derivada, bem como sua incerteza
, derivada, bem como sua incerteza  . O cálculo de
. O cálculo de  é simples, basta substituir o valor de
é simples, basta substituir o valor de  na função
na função  . Mas como eu calculo
. Mas como eu calculo  conhecendo
conhecendo  ? Para isso precisamos aprender a fazer propagações de incertezas. O objetivo deste texto é deduzir uma expressão para propagação de incertezas e discutir alguns exemplos simples.
? Para isso precisamos aprender a fazer propagações de incertezas. O objetivo deste texto é deduzir uma expressão para propagação de incertezas e discutir alguns exemplos simples.
Fórmula geral de propagação de incertezas
Em um caso geral, digamos que eu tenho medidas de vários observáveis (por exemplo, altura e largura de uma folha de papel) e quero calcular uma grandeza derivada (por exemplo, a área desta folha). Conheço as incertezas dessas medidas e quero calcular a incerteza na grandeza derivada (por exemplo, a incerteza na área da folha). Para estabelecer uma notação, vamos denominar as grandezas observáveis como sendo  e a grandeza derivada como sendo
e a grandeza derivada como sendo  , que pode ser calculada através do uso de uma fórmula
, que pode ser calculada através do uso de uma fórmula  . Neste caso,
. Neste caso, 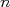 é o número de grandezas observáveis que tenho à disposição.
é o número de grandezas observáveis que tenho à disposição.
Na força bruta, para calcular a incerteza em  , simplesmente repetiríamos a medida do conjunto
, simplesmente repetiríamos a medida do conjunto  um determinado número de vezes (
um determinado número de vezes ( ) e calcularíamos
) e calcularíamos 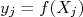 para cada repetição. No final, a variância (quadrado do desvio padrão) de
para cada repetição. No final, a variância (quadrado do desvio padrão) de  poderia ser calculado como:
poderia ser calculado como:

 . Porém, conhecemos o conjunto de incertezas das grandezas
. Porém, conhecemos o conjunto de incertezas das grandezas 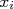 , dado por
, dado por  . Para calcular a incerteza em
. Para calcular a incerteza em  vamos admitir que as incertezas em
vamos admitir que as incertezas em 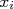 são pequenas o suficiente para que possamos aproximar a função
são pequenas o suficiente para que possamos aproximar a função 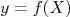 por uma reta por em torno de
por uma reta por em torno de 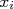 em um intervalo da ordem de
em um intervalo da ordem de  para mais e para menos. A inclinação desta reta ao longo da variável
para mais e para menos. A inclinação desta reta ao longo da variável 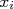 é dada pela derivada parcial de
é dada pela derivada parcial de  em relação à
em relação à 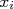 (ver figura 2). Deste modo, podemos escrever a função
(ver figura 2). Deste modo, podemos escrever a função  como sendo, aproximadamente:
como sendo, aproximadamente:

Figura 2 – Aproximação de uma função por uma reta em um ponto qualquer e como uma variação em x gera uma variação em y.
A equação desta reta é:

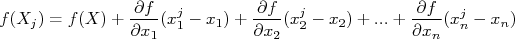
 é aquele calculado em
é aquele calculado em  , ou seja,
, ou seja,  . Substituindo isso, bem como a expansão em série de Taylor, na expressão para o desvio padrão de
. Substituindo isso, bem como a expansão em série de Taylor, na expressão para o desvio padrão de  , temos que:
, temos que:
 |
 |
 |
|
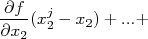 |
|
 |
|
 |
Expandindo o quadrado na somatória, temos:
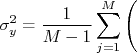 |
 |
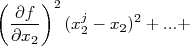 |
|
 |
|
 |
|
 |
Como as derivadas são constantes para a somatória, podemos rearranjar a expressão acima de forma que:
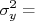 |
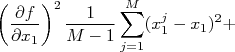 |
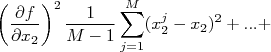 |
|
 |
|
 |
|
 |
|
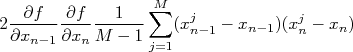 |
Na expressão acima, temos dois tipos de somatória. O primeiro deles tem a forma:

 ) do observável
) do observável 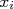 .
.
O segundo tipo de somatória tem a forma:

 ) e será discutido em momento oportuno.
) e será discutido em momento oportuno.
Substituindo essas definições de variância e covariância, temos que:

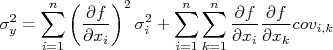
 forem todos independentes um do outro, os termos de covariância são nulos e a expressão acima fica mais simplificada na forma:
forem todos independentes um do outro, os termos de covariância são nulos e a expressão acima fica mais simplificada na forma:
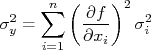
Um exemplo
Vamos dizer que alguém mediu tempo de queda de um balão de uma altura  e obteve que
e obteve que 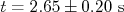 . Usando um modelo simples de queda livre, pode-se deduzir que a aceleração vale:
. Usando um modelo simples de queda livre, pode-se deduzir que a aceleração vale:
 .
. e
e  na expressão acima obtém-se que
na expressão acima obtém-se que  . Qual a incerteza na aceleração? Os nossos observáveis, neste caso, são
. Qual a incerteza na aceleração? Os nossos observáveis, neste caso, são  e
e  e são medidos independentemente, de forma que a covariância entre eles é nula. Assim, podemos escrever que a incerteza em
e são medidos independentemente, de forma que a covariância entre eles é nula. Assim, podemos escrever que a incerteza em  ao quadrado vale:
ao quadrado vale:



de modo que, substituindo essas derivadas na expressão para a incerteza, temos:

 ,
,  ,
,  e
e  ),e obter que:
),e obter que:


Outro exemplo
Alguém mediu o tamanho de uma sala e obteve para a largura e comprimento, respectivamente,  e
e  . A área desta sala é
. A área desta sala é  . Qual a incerteza nesta área? A área depende de duas medidas, a largura e o comprimento, de modo que a incerteza na área é:
. Qual a incerteza nesta área? A área depende de duas medidas, a largura e o comprimento, de modo que a incerteza na área é:
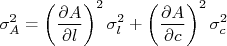


de modo que, substituindo essas derivadas na expressão para a incerteza, temos:


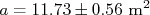
Exercícios
- Mostre que, se
 ou
ou  , a incerteza em
, a incerteza em  pode ser escrita como:
pode ser escrita como:  .
. - Mostre que, se
 ou
ou  , a incerteza em
, a incerteza em  pode ser escrita como:
pode ser escrita como:  .
. - O volume,
 de uma esfera pode ser obtido a partir do seu diâmetro
de uma esfera pode ser obtido a partir do seu diâmetro  , determinado experimentalmente. Mostrar que a incerteza no volume pode ser obtida da expressão:
, determinado experimentalmente. Mostrar que a incerteza no volume pode ser obtida da expressão:  .
. - O ângulo de Brewster de um material foi medido experimentalmente e obteve-se
 . O índice de refração deste material pode ser obtido a partir da expressão
. O índice de refração deste material pode ser obtido a partir da expressão  . Obtenha o valor do índice de refração e sua incerteza.
. Obtenha o valor do índice de refração e sua incerteza. - Uma caixa retangular tem largura, altura e profundidade, respectivamente (em cm):
 ,
,  e
e  . Determine o volume desta caixa e sua incerteza.
. Determine o volume desta caixa e sua incerteza. - Um pêndulo de comprimento
 teve o seu período de oscilação medido em
teve o seu período de oscilação medido em  com o objetivo de determinar o valor da aceleração da gravidade. Sabendo que o período de um pêndulo simples pode ser dado por
com o objetivo de determinar o valor da aceleração da gravidade. Sabendo que o período de um pêndulo simples pode ser dado por 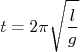 , determine a aceleração da gravidade
, determine a aceleração da gravidade  e sua incerteza.
e sua incerteza. - A velocidade de queda de um paraquedista pode ser calculada por
 onde
onde  é o instante de tempo,
é o instante de tempo,  é a aceleração da gravidade,
é a aceleração da gravidade,  é a massa do paraquedista e
é a massa do paraquedista e  é uma constante que estabelece o arrasto do paraquedas. Calcule a velocidade de queda do paraquedista, com sua incerteza, para
é uma constante que estabelece o arrasto do paraquedas. Calcule a velocidade de queda do paraquedista, com sua incerteza, para  .
.
Deixe um comentário