nA função gaussiana é uma importante função de densidade de probabilidade, muito presente na física experimental. Ela tem a forma de um sino com a boca virado para baixo segundo a expressão:n
n n
n
n
n
 corresponde ao desvio padrão da distribuição e
corresponde ao desvio padrão da distribuição e 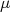 , o seu valor médio. A figura 1 mostra a distribuição gaussiana. n
, o seu valor médio. A figura 1 mostra a distribuição gaussiana. nn

nFigura 1 – Função densidade de probabilidade gaussiana.
n
n
 entre esses limites. Em particular
entre esses limites. Em particular  pode assumir um valor entre
pode assumir um valor entre  e
e  com, aproximadamente, 68% de probabilidade.
com, aproximadamente, 68% de probabilidade.
n
nNeste texto vamos mostrar algumas características da função gaussiana, o porque ela é tão presente na física experimental e uma maneira (dentre várias) de inferir a sua expressão matemática.
n
n
O Teorema do Limite Central
nO Teorema do Limite Central é um dos teoremas fundamentais da teoria de probabilidade e, em linhas gerais pode ser enunciado como:
n
n Em uma amostra aleatória qualquer simples  de elementos independentes entre si, com distribuições de probabilidade bem definida com variância
de elementos independentes entre si, com distribuições de probabilidade bem definida com variância  e média
e média 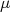 , na medida em que
, na medida em que 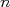 aumenta, a distribuição de probabilidades do valor médio dessa amostra aproxima-se de uma distribuição gaussiana de valor médio
aumenta, a distribuição de probabilidades do valor médio dessa amostra aproxima-se de uma distribuição gaussiana de valor médio 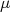 e variância
e variância  .
.
n
nEsse teorema tem um grande impacto na física experimental em particular e explica porque a grande maioria das distribuições de grandezas experimentais apresentam uma distribuição gaussiana. Sabemos que toda medida tem um erro associado a ela. Esse erro é, em geral, composto da soma de um número muito grande de pequenos erros individuais, em geral, independentes. Por conta disso e, aplicando o teorema do limite central, a distribuição de probabilidade dessa medida experimental acaba seguindo uma distribuição gaussiana.
n
nEsse teorema não é simples de ser provado no nível do curso de Física Experimental II. Mas para quem estiver interessado há uma demonstração formal neste link. Contudo, podemos fazer uma “demonstração” empírica a partir de um experimento virtual simples: jogar moedas.
n
nUma moeda tem duas faces: cara e coroa. Para fins matemáticos, vamos assumir que cara tem valor 1 e coroa tem valor -1. Se jogarmos uma moeda, podemos obter cara ou coroa, ou seja, 1 ou -1. Para cada moeda jogada, verificamos qual face obtemos e preenchemos um histograma com o seu valor numérico (1 ou -1). Depois de repetir esse experimento 10000 vezes, obteremos aproximadamente 5000 vezes 1 e outras 5000 vezes, -1, conforme mostra a figura 2.
n
n

nFigura 2 – Cara ou coroa.
n
n
n
n

nFigura 3 – Duas moedas.
n
n
n
n

nFigura 4 – Três moedas.
n
n
n
n

nFigura 5 – 5000 moedas.
n
n
n
n
Inferência da expressão da distribuição Gaussiana
nHá alguns anos eu topei com uma dedução da expressão para a gaussiana a partir de princípios muito simples. Eu não encontrei mais a referência (se alguém descobrir me avise) então resolvi reproduzir esta dedução aqui. Acredito que esta não é uma dedução muito formal como a que encontramos em geral em livros de estatística e sim uma forma de inferir a fórmula da gaussiana a partir de um experimento imaginário simples. Uma dedução mais formal, onde fica claro o teorema do limite central, pode ser encontrada no livro Tratamento Estatístico de Dados em Física Experimental, do Otaviano Helene e Vito Vanin, no capítulo IV.n
nVamos partir de princípios simples, tentando imaginar um experimento que consiste em atirar flechas contra um alvo. A mosca deste alvo é a origem de um plano cartesiano x-y. Contudo, por conta da precisão do arqueiro, nem sempre se consegue acertar a mosca. Vamos assumir que:n
n
- n
- Não há problemas de acurácia, ou seja, o arqueiro, em média, acerta a mosca.n
- Acertar longe da mosca é menos provável que acertar perto.n
- Os erros da posição que a flecha atinge o alvo são independentes, ou seja, uma boa precisão na posição no eixo x não significa uma boa precisão no eixo y, e vice-versa.n
- Os erros da posição que a flecha atinge o alvo não dependem da orientação do plano cartesiano. Isto é, tanto faz qual é a direção e sentido dos eixos x e y.n
n
nUm esquema desse experimento imaginário é mostrado na figura 6.
n
n

nFigura 6 – Esquema do experimento imaginário do artirador, bem como representação de grandezas utilizadas no texto.
n
n
 e
e 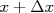 pode ser calculada a partir da função densidade de probabilidade em
pode ser calculada a partir da função densidade de probabilidade em  ,
,  e vale
e vale 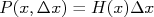 , desde que
, desde que  não varie muito no intervalo
não varie muito no intervalo  . O mesmo pode ser aplicado ao eixo y e a probabilidade de acertar uma região entre
. O mesmo pode ser aplicado ao eixo y e a probabilidade de acertar uma região entre  e
e  é
é 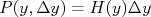 .n
.n
nDeste modo, a probabilidade de acertar uma pequena região quadrada do alvo, de larguras  e
e  , na posição
, na posição  em relação à origem é o produto das duas probabilidades, já que os erros em cada eixo são independentes, ou seja,
em relação à origem é o produto das duas probabilidades, já que os erros em cada eixo são independentes, ou seja,  .n
.n
n
nO produto  corresponde à função densidade de probabilidade de acertar a posição
corresponde à função densidade de probabilidade de acertar a posição  e depende somente da distância à origem, uma vez que a orientação dos eixos cartesianos não afeta a probabilidade final do arqueiro acertar uma posição do alvo. Sendo assim, eu posso orientar esses eixos em qualquer direção. Uma rotação qualquer desses eixos em torno da origem por um ângulo
e depende somente da distância à origem, uma vez que a orientação dos eixos cartesianos não afeta a probabilidade final do arqueiro acertar uma posição do alvo. Sendo assim, eu posso orientar esses eixos em qualquer direção. Uma rotação qualquer desses eixos em torno da origem por um ângulo  qualquer não deve mudar o valor de
qualquer não deve mudar o valor de  . Isso significa que:n
. Isso significa que:n
n
 n
n
n
n
n
 n
n
n
n
 , cartesiana, para
, cartesiana, para  , polares, é bastante simples, ou seja:n
, polares, é bastante simples, ou seja:nn

n n
n
n
n
n

n
n
n
n
 em
em  obtem-se que:n
obtem-se que:nn
 n
n
n
n
n
 n
n
n
n
n
 n
n
n
n
 é uma constante. Portanto, para achar
é uma constante. Portanto, para achar  e
e  devemos resolver as equações:n
devemos resolver as equações:nn
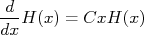
n
n n
n
n
n
n
 n
n
n
n
 deve ser negativa pois a probabilidade deve diminuir na medida em que x (ou y) aumenta. Deste modo podemos reescrever a expressão acima como:nn
deve ser negativa pois a probabilidade deve diminuir na medida em que x (ou y) aumenta. Deste modo podemos reescrever a expressão acima como:nnn
 n
n
n
n
 e
e 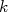 . O valor de
. O valor de  é facilmente determinado sabendo-se que a integral da função densidade de probabilidade em todo espaço vale 1. Assim:n
é facilmente determinado sabendo-se que a integral da função densidade de probabilidade em todo espaço vale 1. Assim:nn
 n
n
n
n
n
 n
n
n
n
n
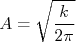 n
n
n
n
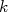 . Podemos fazer isso através da definição de variância:n
. Podemos fazer isso através da definição de variância:nn
 é o valor verdadeiro de uma grandeza. No nosso caso é zero, já que a mosca está posicionada na origem do nosso sistema cartesiano. Para uma distribuição contínua de possibilidades, a média acima é escrita em termos da função densidade de probabilidade como:n
é o valor verdadeiro de uma grandeza. No nosso caso é zero, já que a mosca está posicionada na origem do nosso sistema cartesiano. Para uma distribuição contínua de possibilidades, a média acima é escrita em termos da função densidade de probabilidade como:nn
 n
n
n
n
n
 n
n
n
n
 e
e 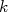 na expressão para
na expressão para  chegamos, finalmente, à:n
chegamos, finalmente, à:nn
 n
n
n
n
 . A generalização para valor verdadeiro (
. A generalização para valor verdadeiro (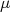 ) diferente de zero corresponde somente a uma translação da origem do eixo no plano cartesiano por esse valor, ou seja:n
) diferente de zero corresponde somente a uma translação da origem do eixo no plano cartesiano por esse valor, ou seja:nn
 n
n
n
n
Deixe um comentário