Fazer gráficos de um observável em função de outro é bastante comum no dia a dia da pesquisa com o objetivo de se extrair alguma informação deste conjunto de dados. Por exemplo, de um gráfico de velocidade em função do tempo para a queda de um objeto pode-se extrair a aceleração do objeto. Do gráfico da massa em função do volume pode-se extrair a densidade do material. Os exemplos são muitos. Uma vez que os dados estão graficados, a extração das informações relevantes é feita através do ajuste de uma expressão matemática, ou função, a estes dados onde os parâmetros desta função correspondem à grandezas de interessa, tais como a aceleração, densidade, etc. Isso pode ser feito visualmente, com uma régua e intuição, mas atualmente é muito mais simples utilizar programas de análise gráfica. Há muitos disponíveis por ai. Como isso é feito? Qual o procedimento matemático que é utilizado para se determinar qual é o melhor conjunto de parâmetros que, em uma função matemática qualquer, descreve o comportamento dos dados da melhor forma possível? Há vários métodos estatísticos disponíveis. Vamos abordar o método dos mínimos quadrados.nnFazer gráficos de um observável em função de outro é bastante comum no dia a dia da pesquisa com o objetivo de se extrair alguma informação deste conjunto de dados. Por exemplo, de um gráfico de velocidade em função do tempo para a queda de um objeto pode-se extrair a aceleração do objeto. Do gráfico da massa em função do volume pode-se extrair a densidade do material. Os exemplos são muitos. Uma vez que os dados estão graficados, a extração das informações relevantes é feita através do ajuste de uma expressão matemática, ou função, a estes dados onde os parâmetros desta função correspondem à grandezas de interessa, tais como a aceleração, densidade, etc. Isso pode ser feito visualmente, com uma régua e intuição, mas atualmente é muito mais simples utilizar programas de análise gráfica. Há muitos disponíveis por ai. Como isso é feito? Qual o procedimento matemático que é utilizado para se determinar qual é o melhor conjunto de parâmetros que, em uma função matemática qualquer, descreve o comportamento dos dados da melhor forma possível? Há vários métodos estatísticos disponíveis. Vamos abordar o método dos mínimos quadrados.
n
n
O método dos mínimos quadrados
nConsidere um conjunto de dados  onde
onde  são incertezas na variável
são incertezas na variável  (mais a frente vamos ver como tratar casos onde há incertezas também em
(mais a frente vamos ver como tratar casos onde há incertezas também em  ). Podemos fazer um gráfico de
). Podemos fazer um gráfico de  em função de
em função de  , obtendo algo similar à figura 1.
, obtendo algo similar à figura 1.
n
n

nFigura 1 – Gráfico de  em função de xnn.
em função de xnn.
nn
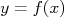 que descreva, estatisticamente, o conjunto de dados tomados, como mostrado na figura 2. Nesta figura,
que descreva, estatisticamente, o conjunto de dados tomados, como mostrado na figura 2. Nesta figura,  , é uma reta e, neste caso, queremos encontrar os valores de
, é uma reta e, neste caso, queremos encontrar os valores de  e
e  que melhor descrevem estes dados.
que melhor descrevem estes dados.
n
n

nFigura 2 – Ajuste de uma reta.
nn
 e
e  que descrevem os dados. Por exemplo, na figura 3, vemos o mesmo conjunto de dados com uma reta que claramente não descreve o comportamento médio dos dados experimentais.
que descrevem os dados. Por exemplo, na figura 3, vemos o mesmo conjunto de dados com uma reta que claramente não descreve o comportamento médio dos dados experimentais.
n
n

nFigura 3 – Reta com valores de  e
e  que não descrevem os dados.
que não descrevem os dados.
nn
 e
e  ? O método dos mínimos quadrados consiste em um dos métodos disponíveis para fazer esta determinação. Ele se baseia no princípio da máxima verossimilhança que, em linhas gerais, consiste em determinar os valores desses coeficientes que maximizem a probabilidade dos dados serem compatíveis com a função que está sendo ajustada.
? O método dos mínimos quadrados consiste em um dos métodos disponíveis para fazer esta determinação. Ele se baseia no princípio da máxima verossimilhança que, em linhas gerais, consiste em determinar os valores desses coeficientes que maximizem a probabilidade dos dados serem compatíveis com a função que está sendo ajustada.
n
nVamos olhar então o nosso conjunto de dados  , que consiste em
, que consiste em 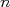 pontos
pontos  , independentes um do outro. Além disso, os valores de
, independentes um do outro. Além disso, os valores de  possuem funções densidade de probabilidade gaussianas em relação ao seu valor verdadeiro
possuem funções densidade de probabilidade gaussianas em relação ao seu valor verdadeiro 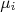 com desvio padrão
com desvio padrão  . Os valores verdadeiros
. Os valores verdadeiros  dependem do valor de
dependem do valor de 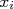 . Neste caso, a probabilidade de se fazer uma medida
. Neste caso, a probabilidade de se fazer uma medida  é proporcional à esta função densidade de probabilidade, ou seja:
é proporcional à esta função densidade de probabilidade, ou seja:
n
n

n
n
nQueremos estimar, da melhor forma possível, os valores verdadeiros  de tal forma que a probabilidade seja máxima. Vamos tentar descrever os valores verdadeiros por uma função
de tal forma que a probabilidade seja máxima. Vamos tentar descrever os valores verdadeiros por uma função  , que depende de
, que depende de  , com
, com 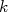 parâmetros
parâmetros  , a serem determinados, ou seja:
, a serem determinados, ou seja:
n
n

n
n
 e
e  e
e  . Assim, a a probabilidade de se fazer uma medida
. Assim, a a probabilidade de se fazer uma medida  pode ser escrita como:n
pode ser escrita como:n
n
n
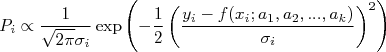
n
n
nA probabilidade total de encontrarmos o conjunto de dados medido consiste no produto da probabilidade de medir cada ponto  , ou seja:n
, ou seja:n
n
n
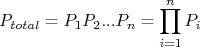
n
n
n
nn
n
nnConcluimos que a expressão para a probabilidade total é:n
n
n
 n
n
n
n
 seja máxima se o valor da somatória:n
seja máxima se o valor da somatória:n
n
n
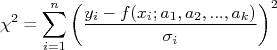
n
n
 , é chamada de chi-quadrado.
, é chamada de chi-quadrado.
n
nAjustar uma função a um conjunto de dados consiste, então, em determinar os valores dos parâmetros  , conhecendo-se a fórmula para
, conhecendo-se a fórmula para 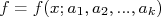 de modo a minimizar o valor para
de modo a minimizar o valor para  . Esté é o chamado método dos mínimos quadrados. Note que fizemos duas suposições importantes: a primeira é que os pontos
. Esté é o chamado método dos mínimos quadrados. Note que fizemos duas suposições importantes: a primeira é que os pontos  são independentes um dos outros de modo que podemos calcular a probabilidade total como o produto das probabilidades individuais e elas são calculadas independentemente uma das outras. A segunda, mais importante, é que as funções densidade de probabilidade de cada ponto são gaussianas. Sem esta condição, nem sempre é possível maximizar a probabilidade minimizando o
são independentes um dos outros de modo que podemos calcular a probabilidade total como o produto das probabilidades individuais e elas são calculadas independentemente uma das outras. A segunda, mais importante, é que as funções densidade de probabilidade de cada ponto são gaussianas. Sem esta condição, nem sempre é possível maximizar a probabilidade minimizando o  .n
.n
n
n
O método dos mínimos quadrados (MMQ) aplicado a alguns casos
nVamos então aplicar o método dos mínimos quadrados em alguns casos simples:
n
n
- n
-
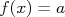 , ou seja, uma função constante;n
, ou seja, uma função constante;n
-
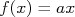 , ou seja, uma reta passando na origem;n
, ou seja, uma reta passando na origem;n
-
 , ou seja, uma reta qualquer.n
, ou seja, uma reta qualquer.n
n
n
O MMQ para uma constante
nImagine um gráfico como o da figura 4. Aparentemente  é uma constante, independentemente dos valores de
é uma constante, independentemente dos valores de  . Neste caso,
. Neste caso, 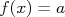 pode ser uma boa expressão para descrever os dados acima. n
pode ser uma boa expressão para descrever os dados acima. n
n
n

nFigura 4 – Alguns dados a serem ajustados.
n
n
 que maximize a probabilidade de
que maximize a probabilidade de 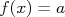 descrever os dados obtidos, utilizando o método dos mínimos quadrados. Para isso, devemos minimizar o valor de
descrever os dados obtidos, utilizando o método dos mínimos quadrados. Para isso, devemos minimizar o valor de  . Substituindo
. Substituindo  na expressão para o
na expressão para o  , temos:n
, temos:n
n
n
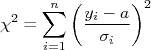
n
n
 que minimize o
que minimize o  devemos fazer:n
devemos fazer:n
n
n
 n
n
n
n
n
n
 n
n
n
n
n
n
 n
n
n
n
 , chegamos à:n
, chegamos à:n
n
n
 n
n
n
n
 , que resulta em:n
, que resulta em:n
n
n
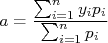 n
n
n
n
 corresponde à média dos valores de
corresponde à média dos valores de  ponderados pelo inverso do quadrado das incertezas. Isso é razoável de se entender: pontos com incertezas pequenas (mais precisos) possuem peso maior e, neste caso, o valor de
ponderados pelo inverso do quadrado das incertezas. Isso é razoável de se entender: pontos com incertezas pequenas (mais precisos) possuem peso maior e, neste caso, o valor de  vai ficar mais próximo desses pontos. Pontos com elevada incerteza possuem pouco peso e, consequentemente, são pouco considerados no cálculo da média.
vai ficar mais próximo desses pontos. Pontos com elevada incerteza possuem pouco peso e, consequentemente, são pouco considerados no cálculo da média.
n
nNa figura 5 mostramos a função ajustada aos dados da figura 4. Note como os dados ficam distribuídos em torno da constante ajustada.
n
n

nFigura 5 – Constante ajustada aos dados.
n
n
 , que pode ser isolado para fora das somatórias, resultando em:n
, que pode ser isolado para fora das somatórias, resultando em:n
n
n
 n
n
n
n
 .n
.n
nn
O MMQ para uma reta passando na origem
nImagine agora a situação na qual a função que queremos ajustar aos dados seja uma reta que passa na origem, 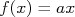 . Devemos então achar a constante
. Devemos então achar a constante  , que é o coeficiente angular da reta, utilizando o MMQ. Neste caso, o
, que é o coeficiente angular da reta, utilizando o MMQ. Neste caso, o  pode ser escrito como:n
pode ser escrito como:n
n
n
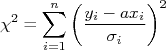
n
n
 e a utilizada no caso anterior. Mais uma vez, a minimização do
e a utilizada no caso anterior. Mais uma vez, a minimização do  para encontrar a constante
para encontrar a constante  ocorre quando:n
ocorre quando:n
n
n
 n
n
n
n
n
n

n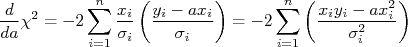 n
n
n
n
 temos que:n
temos que:n
n
n

n
n
n
n
n
n
n

n
n
n
O MMQ para uma reta qualquer
nNo caso de uma reta genérica,  , devemos encontrar os valores de
, devemos encontrar os valores de  e
e  que minimizam, simultaneamente, o
que minimizam, simultaneamente, o  dos dados obtidos em relação a esta função. Seguindo os exemplos anteriores, a expressão para o
dos dados obtidos em relação a esta função. Seguindo os exemplos anteriores, a expressão para o  pode ser escrita como:n
pode ser escrita como:n
n
n

n
n
 e
e  fazemos então:n
fazemos então:n
n
n

n
n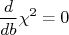 n
n
n
n
 e
e  . Então não há problemas. A única diferença e o maior grau de dificuldade algébrica, neste caso.
. Então não há problemas. A única diferença e o maior grau de dificuldade algébrica, neste caso.
n
nVou deixar como exercício a resolução das duas derivadas acima e também a resolução do sistema de equações que surge. É muito interessante que isso seja feito com calma e atenção. O MMQ é uma importante ferramenta de análise de dados e vai estar presente no dia a dia nosso. Resolvendo o sistema de equações encontra-se que:n
n
n
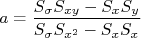
n
n n
n
n
n
 somatórias definidas como:n
somatórias definidas como:n
n
n
 n
n
n
n n
n
n
n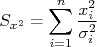 n
n
n
n n
n
n
n n
n
n
n
n
n

nFigura 6 – Ajuste de uma reta a pontos experimentais.
n
n
Incerteza dos parâmetros ajustados
nNote que, como os parâmetros das funções são extraídos de um conjunto de dados, é natural pensar que flutuações estatísticas neste conjunto de dados afetem os valores dos parâmetros ajustados. Se repetirmos o mesmo experimento, com o mesmo procedimento, várias vezes, é natural imaginar que, a cada vez, um conjunto de parâmetros diferente será extraído. Ou seja, os parâmetros extraídos também estão sujeitos a flutuações e, consequentemente, possuem incertezas. Como obter as incertezas dos parâmetros ajustados?
n
nA incerteza dos parâmetros ajustados pode ser obtida através de propagação de incertezas. Sendo uma função  onde cada medida
onde cada medida  possui uma incerteza
possui uma incerteza  , a incerteza de
, a incerteza de  pode ser calculada através de:n
pode ser calculada através de:n
n
n

n
n
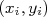 e das incertezas nos pontos,
e das incertezas nos pontos,  . Nesse caso, considerando que há apenas incertezas nos valores de
. Nesse caso, considerando que há apenas incertezas nos valores de  (veremos mais a frente o que fazer quando há incertezas em
(veremos mais a frente o que fazer quando há incertezas em  ). Não consideramos também que as incertezas são estimadas e, portanto, também estariam sujeitas a flutuações. Sendo assim, devemos aplicar a fórmula de propagação de incertezas somente em relação aos valores de
). Não consideramos também que as incertezas são estimadas e, portanto, também estariam sujeitas a flutuações. Sendo assim, devemos aplicar a fórmula de propagação de incertezas somente em relação aos valores de  dos dados ajustados.
dos dados ajustados.
n
nn
Incerteza no ajuste de uma constante
nComo vimos acima, se fizermos um ajuste de uma constante, ou seja, 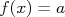 , aos dados, o MMQ resulta em:
, aos dados, o MMQ resulta em:
n
n
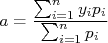
n
n
 . Neste caso, aplicando-se a fórmula de propagação de incertezas, temos que:n
. Neste caso, aplicando-se a fórmula de propagação de incertezas, temos que:n
n
n

n
n
 , obtemos que:n
, obtemos que:n
n
n

n
n
n
n
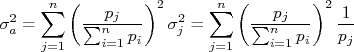
n
n
n
n
 n
n
n
 , ela se reduziria à:n
, ela se reduziria à:n
n
n
 n
n
n
n
nn
Incerteza no ajuste de uma reta passando pela origem
nNo caso de um ajuste de uma reta passando na orígem, 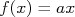 , a constante
, a constante  , conforme deduzimos, vale:n
, conforme deduzimos, vale:n
n
n

n
n
n
 vale:n
vale:n
n
n

n
n
n
n
n

n
n
n
Incerteza no ajuste de uma reta qualquer
nNo caso de uma reta qualquer,  , os parâmetros ajustados são dados por:n
, os parâmetros ajustados são dados por:n
n
n
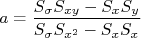
n
n n
n
n
n
 somatórias definidas anteriormente. Usando o mesmo princípio que nos casos anteriores de propagação de incertezas, considerando apenas as grandezas
somatórias definidas anteriormente. Usando o mesmo princípio que nos casos anteriores de propagação de incertezas, considerando apenas as grandezas  como possuindo incertezas, é fácil chegar em (faça como exercício):n
como possuindo incertezas, é fácil chegar em (faça como exercício):n
n
n

n
n n
n
n
n
 , por exemplo, força que o valor de
, por exemplo, força que o valor de  diminua de modo a tentar manter o
diminua de modo a tentar manter o  minimizado. E vice-versa: uma diminuição de
minimizado. E vice-versa: uma diminuição de  força um aumento em
força um aumento em  . Ou seja, estes parâmetros não são independentes. Em momento oportuno eu pretendo escrever um texto mais formal sobre covariâncias e tocarei neste assunto novamente. Por hora, caso seja necessário, a covariância entre esses parâmetros pode ser facilmente calculada através de:n
. Ou seja, estes parâmetros não são independentes. Em momento oportuno eu pretendo escrever um texto mais formal sobre covariâncias e tocarei neste assunto novamente. Por hora, caso seja necessário, a covariância entre esses parâmetros pode ser facilmente calculada através de:n
n
n
 n
n
n
n
Ajustes com incertezas na variável x
n O MMQ que desenvolvemos até aqui supôs que  ou seja, não há incertezas nas variáveis
ou seja, não há incertezas nas variáveis  . Mas em muitas situações práticas, tanto as variáveis
. Mas em muitas situações práticas, tanto as variáveis  quanto
quanto  possuem incertezas. O método formal para isso é chamado de método dos mínimos quadrados totais (ver esse link). Vamos aqui tentar simplificar um pouco e tentar compreender a ideia por trás de uma minimização onde consideramos incertezas em
possuem incertezas. O método formal para isso é chamado de método dos mínimos quadrados totais (ver esse link). Vamos aqui tentar simplificar um pouco e tentar compreender a ideia por trás de uma minimização onde consideramos incertezas em  e
e  .
.
n
nNo MMQ somente com incertezas em  nós calculamos os resíduos entre os pontos experimentais e a função ajustada, dados por:n
nós calculamos os resíduos entre os pontos experimentais e a função ajustada, dados por:n
n
n n
n
n
n
n
n n
n
n
n
 .n
.n
n
nO que estamos fazendo, quando obtemos os resíduos desta forma, é calcular a “distância” entre os pontos experimentais e a função ajustada em unidades de incerteza. Quando só há incerteza em  , a incerteza da diferença entre
, a incerteza da diferença entre  e
e 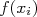 é dada pela própria incerteza em
é dada pela própria incerteza em  ou seja,
ou seja,  .
.
n
nQuando há incerteza em 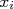 , a o valor da função em
, a o valor da função em 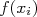 está sujeita a uma incerteza. Sabendo que a diferença entre o ponto experimental e a função ajustada pode ser escrita como:n
está sujeita a uma incerteza. Sabendo que a diferença entre o ponto experimental e a função ajustada pode ser escrita como:n
n
n n
n
n
n
n
n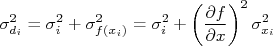 n
n
n
n
n
n n
n
n
n
n
n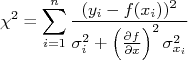 n
n
n
n
 . Note que isso é agora muito mais complexo, pois há um termo de uma derivada de
. Note que isso é agora muito mais complexo, pois há um termo de uma derivada de  , o que complica bastante a resolução algébrica do problema. Programas de computadores lidam com isso sem muitos problemas, seja resolvendo precisamente o problema de mínimos quadrados totais, seja através de métodos numéricos. Por outro lado, podemos nos encontrar em uma situação na qual não temos à disposição um programa para fazer a regressão total ou o que temos considera apenas incertezas em
, o que complica bastante a resolução algébrica do problema. Programas de computadores lidam com isso sem muitos problemas, seja resolvendo precisamente o problema de mínimos quadrados totais, seja através de métodos numéricos. Por outro lado, podemos nos encontrar em uma situação na qual não temos à disposição um programa para fazer a regressão total ou o que temos considera apenas incertezas em  . Neste caso, podemos aplicar uma receita simples que funciona na grande maioria dos casos práticos do nosso dia a dia:n
. Neste caso, podemos aplicar uma receita simples que funciona na grande maioria dos casos práticos do nosso dia a dia:n
n
n
- n
- Faça o ajuste da função considerando apenas as incertezas em
 , ou seja, assuma que
, ou seja, assuma que  .n
.n
- De posse dos parâmetros ajustados, calcule incertezas “efetivas” para
 dadas por:
dadas por: 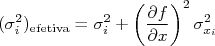 n
n
- Faça novamente o ajuste da função considerando agora que as incertezas em
 são as efetivas, calculadas no passo (2).n
são as efetivas, calculadas no passo (2).n
- De posse dos novos parâmetros ajustados, repita os passos (2) e (3) até que a diferença entre uma repetição e a anterior para os valores dos parâmetros ajustados seja pequeno, se comparada à incerteza desses parâmetros. n
n
nnÉ um método trabalhoso mas com uma ou duas interações, em geral, a resposta converge e o resultado é bastante satisfatório do ponto de vista prático.
Deixe um comentário