Introdução histórica da física de partículas elementares

nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
nO estudo sistemático das partículas elementares começou, de fato, no final do séc. XIX, com a descoberta do elétron, seguindo-se ao fóton, próton, nêutron e todo um zoológico que partículas que foi populado até o nascimento do modelo de quarks e posterior Modelo Padrão. Hoje conhecemos um punhado pequeno de partículas tidas como fundamentais, na escala de energia que podemos testar, do qual conseguimos explicar todo este zoológico construído, principalmente, na primeira metade do séc. XX. Estas partículas são mostradas na figura 1 e são, 6 quarks, 6 léptons e 5 (6, se separarmos o W em W⁺ e W^–) bósons. Para os quarks e léptons temos também suas antipartículas. Se considerarmos que estas partículas possuem números quânticos de cor, este número sobe para 61, ainda um número grande, o que motiva, atualmente, o questionamento se estas partículas são de fato fundamentais ou se elas são originadas de estruturas mais simples. O tempo dirá.
n
n

n

nFigura 1 – Partículas fundamentais (retirado da wikipedia).nn
n
nApesar de ter sido apenas nos últimos séculos que efetivamente avançamos na compreensão da estrutura fundamental da matéria, esta sempre foi uma questão importante para a humanidade. Por conta disso, começarei esta introdução histórica um pouco mais para trás, apenas para listar algumas ideias filosóficas que possuem grande familiaridade com a nossa visão atual.
n
nTalvez a primeira menção sobre a estrutura básica da metéria date de aproximadamente 600 A.C., com a visão de Thales de Mileto de que a água seria a substância mais fundamental. Pouco tempo depois, por volta de 500 A.C., Anaxágoras e Empédocles argumentaram que a criação e destruição de matéria seria devido a diferentes ordenações de partículas invisíveis. Empédocles reduziu esses elementos a quatro: fogo, ar, terra e água. A química nasceu inicialmente com esta concepção. Em ~400 A.C., Demócrito argumentou que o Universo consiste basicamente de espaço vazio e de um número quase infinito de partículas invisíveis e indivisíveis. Nascia a ideia de átomo. O curioso desta argumentação é a questão do espaço vazio que se mostra bastante compatível com a nossa realidade microscópica.
n
nA antiguidade clássica debateu bastante a estrutura do Universo e como nos localizamos nele. Contudo, faltava método de exploração e também meios de investigar. A ciência moderna nasceu muitos séculos depois. No Séc. XI Roger Bacon argumentava que, para entender e aprender os segredos do Universo, devemos primeiro observar. Alguns séculos depois, nascia o método científico moderno, atribuído historicamente à Galileu Galilei, apesar de que alguns documentos arqueológicos mostrarem que, no antigo Egito, realizava-se estudos empíricos sobre diversas áreas da ciência, como Atronomia, Matemática e Medicina.
n
nNo séc. XIX, Dmitri Mendelev, químico russo, organizou os elementos de acordo com suas propriedades, formulando a tabela periódica dos elementos, utilizada até hoje. Apesar de cientificamente correta, ele mostrou uma enorme complexidade e esta complexidade fomenta a ideia de que existe algo mais fundamental que o átomo para descrever o Universo. A ideia da antiguidade grega, por mais errada que esteja, era bastante atraente por sua simplicidade e economia em elementos fundamentais.
n
nO entendimento mais fundamental do Universo é uma busca antiga e constante na evolução humana. A física de partículas moderna teve o seu início no final do séc. XIX, motivada pelo crescente entendimento do eletromagnetismo. Em 1874, Stoney, físico irlandês, sugere que existe uma quantidade básica de eletricidade, dada pela carga elétrica de um íon monovalente, que ele foi capaz de estimar o seu valor. A descoberta do elétron, através do estudo de raios catódicos, teve a contribuição de muitas pessoas diferentes. Um texto interessante sobre isso pode ser lido na wikipedia. Contudo, em 1896, Thomsom e colegas mostraram que os raios catódicos eram partículas mais elementares que átomos e moléculas. Mostraram também que essas partículas não eram ondas eletromagnéticas. Essas partículas possuíam massa da ordem de 1/1000 da massa do hidrogênio e sua natureza independia do material utilizado para criar os raios catódicos. Estava descoberto o elétron, primeira partícula fundamental, na nossa concepção atual. Milikan, posteriormente, realizou medidas da carga do elétron com elevada precisão. Thomsom acreditava que essas partículas tinham origem no interior dos átomos e, portanto, átomos não seriam mais indivisíveis, fundamentais. Contudo, para explicar o caráter eletricamente neutro dos átomos, ele criou um modelo no qual elétrons, negativos, neutralizam a carga positiva também presente nos átomos. Ele criou o modelo de pudim de passas, que se mostrou equivocado alguns anos depois.n
n
nParalelamente à descoberta do elétron, muito estava sendo feito para entender a natureza da luz. Newton propôs uma teoria corpuscular para a luz que, com o desenvolvimento do eletromagnetismo clássico, que culminou nas equações de Maxwell, ficou esquecido. Apesar de o eletromagnetismo de Maxwell ser capaz de explicar muitos dos fenômenos observados, uma série de novas evidências logo mostrou que esta interpretação era apenas parcial. Segundo Maxwell, a energia da luz dependeria apenas da intensidade do campo eletromagnético. Contudo, várias reações químicas fotodependentes ocorriam apenas em algumas frequências luminosas, independentemente da intensidade do campo utilizado. Além disso, havia muita dificuldade de conciliar a visão de Maxwell com o espectro de radiação de corpos aquecidos (corpos negros). Ademais, notava-se que podia-se arrancar elétrons de superfícies metálicas através de injeção de ondas eletromagnéticas (efeito fotoelétrico). Contudo, a energia desses elétrons dependia somente da frequência da luz incidente e não da intensidade do campo eletromagnético. Apesar de Planck ter postulado que o campo eletromagnético é formado por quanta de energia , sendo capaz de explicar o espectro de radiação de corpo negro, foi Einstein que, pouco depois, postulou que esses quanta (os fótons) deveriam possuir momento tal que , assumindo características de partículas. Esta propriedade foi verificada por Compton em 1922, mostrando que fótons possuem comportamento corpuscular. O campo eletromagnético é, então, composto por esses quanta de luz. Esta propriedade, que intrigou Einstein pelo resto de sua vida, ao tentar reconciliar as Eq. de Maxwell com a natureza corpuscular da luz, foi acomodada perfeitamente na teoria quântica para o eletromagnetismo (Eletrodinâmica Quântica) e, posteriormente, pelo Modelo Padrão.
n
nNo séc. XX as coisas começaram a andar relativamente rápido. Muitas informações começaram a surgir dos experimentos que estavam sendo realizados. No começo do século, Rutherford, Geiger e Marsden, através do experimento no qual bombardeavam partículas alfa (hélios desprovido de seus elétrons) mostraram que o modelo de Thomsom estava errado e descobriram que o átomo seria composto de um núcleo, de carga positiva, responsável por praticamente toda a massa do átomo, porém de tamanho tipicamente 10 mil vezes menor que um átomo.
n
nn

nFigura 2 – Esquema do experimento de Rutherford.
n
n

nFigura 3 – Dados obtidos no experimento de Rutherford, bem como previsões teóricas para o modelo de Rutherford e Thomsom.
n
nnNão demorou muito para perceber que, aumentando a energia das partículas alfa, a fórmula de Rutherford começa a falhar, evidenciando que o núcleo atômico possui estrutura interna, conforme mostra a figura 4.
n
nn

nFigura 4 – Aumentando a energia da partícula alfa, a fórmula de Rutherford falha, gerando evidências de que o núcleo não é fundamental.
n
nnEntão, o próprio Rutherford, em 1919, descobriu a existência do próton no interior do núcleo, através de um aparato experimental (figura 5) onde ele detectava a reação nuclear e, em 1930, Chadwick, com um arranjo bastante parecido (figura 6), descobriu a existência do nêutron. Por volta dos anos de 1930, prótons e nêutrons eram tidos como partículas fundamentais e, aparentemente, estava tudo muito bem encaminhado: toda a tabela periódica poderia ser descrita pela combinação de três partículas (prótons, nêutrons e elétrons). Uma visão bem simples e elegante. Prótons e nêutrons foram chamados de bárions, que significa “pesados” e o elétron, lépton, que significa pequeno, leve.n
n
nn

nFigura 5 – Arranjo experimental utilizado para descobrir o próton.
n
n

nFigura 6 – Arranjo experimental utilizado para descobrir o nêutron.n
n
nAinda que o cenário fosse relativamente promissor, ainda havia algumas perguntas que deveriam ser respondidas: a emissão de radiação pelo núcleo e as características da força de interação nuclear, que manteria os prótons e nêutrons juntos no núcleo.
n
nEm 1934, Yukawa previu a existência de mésons (que significa médio) como sendo as partículas responsáveis pela interação forte entre prótons e nêutrons. Uma ideia similar aos quanta de luz, somente que para o campo responsável pela interação nuclear forte. Yukawa previu que um campo escalar de partículas massivas dariam origem a um potencial da forma:
n
n
n
nonde é a massa da partícula que compõe este campo, neste caso, o píon. No caso do fóton, , temos um potencial coulombiano. é um fator de escala que dita a intensidade da interação. Na figura 6 são mostradas diversas curvas de potencial para diferentes valores de massa. Note que, quando maior a massa, menor o alcance do potencial. Conhecendo o alcance da força nuclear é fácil estimar o valor da massa do píon, por volta de (vamos tratar de unidades mais adiante). Esta massa pode ser estimada também a partir do princípio da interceza:n
n
nnnn
n
nn

nFigura 7 – Diferentes curvas de potencial de Yukawa para diferentes valores de massa (fonte wikipedia).
n
nnA interação entre um próton e nêutron seria devida à troca de um píon. A carga deste píon depende do tipo de interação, como mostra a figura 8. Em 1936, Anderson, o mesmo que descobriu o pósitron (daqui a pouco), descobriu o múon. Inicialmente achava-se que ele seria a partícula prevista por Yukawa, mas esta partícula não tinha as propriedades necessárias para tal, além da massa parecida com a prevista. No final, o múon é um lépton, como o elétron. Durante muito tempo chamou-se esta partícula de méson-mu. Até hoje, por vício de linguágem, muitos ainda utilizam esta nomeclatura, principalmente os mais “velhinhos”. Em 1947, realizando medidas de raios cósmicos, Lattes, Occhialini e Powell descobriram o méson-pi, depois da análise cuidadosa de emulsões fotográficas colocadas em elevadas altitudes (figura 9).n
n
nn

nFigura 8 – Mecanismo de interação entre prótons e nêutrons.
n
n

nFigura 9 – Emulsão fotográfica mostrando o decaimento do píon (Nature 159, 694-697).
n
n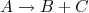nNeste mesmo período, outro problema assombrava os cientistas: o decaimento beta do núcleo. A primeira evidência intrigante no decaimento beta surgiu da medida do espectro de energia para os elétrons emitidos. Em um decaimento genérico de dois corpos , com o núcleo mãe em repouso, podemos escrever que o valor-Q da reação está relacionado às energias cinéticas das partículas filhas através de:nn n
nnDevemos impor a conservação de momento linear. A conservação do momento em decaimentos de dois corpos, aliado à equação acima, faz com que as energias cinéticas das partículas filhas sejam bem definidas. Ademais, no decaimento beta a massa do elétron é muito menor que a massa do núcleo resultante de decaimento. Nesse caso, toda energia liberada pelo decaimento deveria ser convertida em energia cinética do elétron, igual ao valor-Q da reação, como observa-se, por exemplo, para o decaimento alfa, em primeira aproximação. Não foi isso o observado. Na figura 10 mostramos o espectro de elétrons (e pósitrons) medidos para o decaimento beta do núcleo de ⁶⁴Cu. A diferença entre os dados para elétrons e pósitrons vem, em uma visão mais ingênua, do fato de elétrons serem freados após o decaimento devido à interação atrativa com o núcleo resultante enquanto pósitrons são repelidos, pelo mesmo motivo. A energia cinética das partículas beta emitidas apresenta uma larga distribuição, incompatível com o previsto para um decaimento de dois corpos. Esse foi um grande problema para a física nuclear no início do século XX. n n nFigura 10 – Espectro de decaimento β do ⁶⁴Cu.
nnEm 1930, Wolfgang Pauli, em carta submetida a cientistas em uma conferência (figura 11), sugere a existência de uma terceira partícula nesse decaimento. Naquele momento, Pauli chamou essa partícula de nêutron. A descoberta do nêutron por Chadwick, em 1932, com características diferentes das propostas por Pauli, renomeou essa partícula para neutrino. Em tradução (Phillippe Gouffon), temos: “Prezados senhoras e senhores radioativos. Rogo-lhes escutar com muita boa vontade o portador desta carta. Ele lhes dirá em detalhes que, para sanar a má estatística dos núcleos do N e Li6 e o espectro beta contínuo, descobri umnremédio desesperado para salvar as leis de conservação da energia e as estatísticas. Trata-se da possibilidade da existência nos núcleos de partículas neutras de spin 1/2, obedecendo ao principio de exclusão, mas diferentes dos fótons pois elas não se movem à velocidade da luz, e que chamo de nêutrons. A massa dos nêutrons deve ser da mesma ordem de grandeza da dos elétrons e não deve em hipótese nenhuma exceder 0,01 da massa do próton. O espectro beta seria então compreensível se supusermos que durante a desintegração beta, com cada elétron emitido um nêutron seja emitido, de modo que a soma das energias do nêutron e do elétron seja constante.”nn n nFigura 11 – Carta de Wolfgang Pauli, sugerindo a existência do neutrino.
nnEntre a previsão e descoberta passaram-se mais de 30 anos. Neutrinos foram descobertos apenas em 1953, por Cowan e Reines, que ganharam Prêmio Nobel, mais de 40 anos depois, em 1995. Eles usaram como fonte de neutrinos um reator nuclear e como detector, cintilador líquido rico em prótons. De fato, eles observaram a reação inversa . Nesse primeiro experimento (figura 12), a razão de sinal para fundo era de 1/10. Medidas mais precisas, alguns anos depois, com razão sinal/fundo de 4/1, confirmaram essa descoberta. A dificuldade em realizar essa medida vem do fato de neutrinos interagirem apenas por força fraca. De fato, neutrinos podem atravessar a Terra sem sofrer, na maioria das vezes, uma única interação. Medidas experimentais do espectro de energia de elétrons sugerem que neutrinos possuam massa muito pequena, se comparada à própria massa do elétron, inicialmente pensada até como nula. A observação da flutuação de neutrinos, que resolveu o problema de neutrinos solares, no início do século XXI, é uma evidência fundamental para a existência de massa não nula para essas partículas. Voltaremos a esse assunto em um momento oportuno. n n nFigura 12 – Arranjo experimental para detecção de neutrinos utilizado por Reines e Cowan.
nUm outro assunto ocupava tempo dos cientistas na primeira metade do século XX. A conciliação da Relatividade Restrita com a Mecânica Quântica. Em 1926, Klein e Gordon propuseram uma equação que descrevesse quanticamente elétrons relativísticos. Mais tarde percebeu-se que esta equação é apropriada para descrever partículas de spin nulo, como o píon. Ela não serve para elétrons. Uma equação relativística para elétrons foi formulada pouco tempo depois, por Dirac, em 1928 (Proc. R. Soc. Lond. A. 1928 117 610-624). Essas equações, contudo, apresentavam estados possíveis de energia negativa. Dirac formulou uma explicação interessante para estes estados negativos. Ele argumentou que estes estados negativos estariam todos ocupados por um mar de elétrons infinito e impossíveis de serem observados (figura 13). A excitação de um elétron deste mar poderia leva-lo a um nível de energia positiva, passível de observação. Neste caso, um buraco seria deixado neste mar. Este buraco foi interpretado como uma antipartícula desse elétron e, por ser uma falta de carga negativa, seria observado como uma região de carga positiva. Se o elétron voltasse a ocupar este buraco, tanto o elétron como o buraco desapareceriam pois o mar voltaria a ficar preenchido. Estava prevista a existência de uma antipartícula para o elétron, o pósitron. n
n
nn

nFigura 13 – Mar de Dirac e produção de antipartículas.
n
nnEm 1932, Anderson, através da análise de fotografias em câmaras de Wilson, detectou partículas positivas com massa similar a do elétron (figura 14). Foi descoberto o pósitron, a primeira antipartícula. Esta conclusão veio através da análise da curvatura desta partícula antes e depois de atravessar uma placa de chumbo de 6 mm de espessura. O comprimento da trajetória, após atravessar a placa de chumbo, antes da partícula parar, determina sua energia. A curvatura, por conta da presença do campo magnético, determina seu momento e carga. Um próton, de mesma curvatura, não conseguiria ter uma trajetória tão longa quanto a observada.n
n
nn

nFigura 14 – Fotografia de uma câmara de Wilson analisada por Anderson, mostrando um pósitron.
n
nnApesar de Dirac estar preocupado com a descrição relativística do elétron, sua formulação se aplica para qualquer partícula de spin 1/2, incluindo o próton e nêutron. A ideia de mar para essas partículas é igualmente válida. Contudo, o gap de energia para extrair um próton (ou nêutron) do mar de Dirac, 2 m_p c², é muito maior que o para elétrons, 2 m_e c², e a observação destas antipartículas só foi possível com o advento de aceleradores energéticos, por volta dos anos de 1950.
n
nAté meados de 1950 as coisas pareciam acomodadas, apesar de não se entender o papel do múon nas partículas fundamentais. Temos os prótons, nêutrons e elétrons, com suas respectivas antipartículas (apesar de os antiprótons e antineutrons não terem sido observados), os píons explicando as interações fortes e o fóton, como quanta de luz. Em 1947, análise de fotografias de raios cósmicos, Rochester e Butler descobriram uma partícula neutra que decaia em píons positivos e negativos (figura 15), com massa também intermediária entre o píon e o próton. Inicialmente chamada de 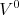, depois de 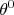, hoje é conhecida como Kaon-0, . Pouco tempo depois, uma outra partícula neutra, desta vez mais pesada que o próton, também foi descoberta. Esta partícula, batizada de lambda , decaia em um próton e um píon-. Esta partícula pertenceria à família dos bárions, partículas pesadas. Estas partículas, por conta de suas características, foram chamadas de partículas estranhas e vieram para “apimentar a festa”.n
n
nn

nFigura 15 – Decaimento de um káon-0.n
n
nnNo final dos anos de 1960, ainda mais com o advento de aceleradores mais potentes, um enorme zoológico de partículas havia sido descoberto (figura 16). A situação parecia a mesma de Mendelev, no final do séc. XIX. Havia uma enorme tabela periódica de partículas “fundamentais” que gerava um enorme desconforto. Ainda para piorar a situação, não parecia haver uma forma lógica de organização dessas partículas segundo suas propriedades, como Mendelev fez com os elementos químicos. A física de partículas estava em crise.n
nn

nFigura 16 – Partículas descobertas na primeira metade do séc. XX.n nnQuem propôs uma solução elegante para organizar estas partículas foi Gell-Mann, em 1961, que introduziu o Eightfold Way. Neste modelo, Gell-Mannn organizou mésons e bárions em figuras geométricas (figuras 17 à 19) através da introdução de um número quântico a mais para estas partículas, a estranheza (S), além da carga elétrica. Nestas figuras, cada linha corresponde a um valor de estranheza e cada diagonal corresponde a um valor de carga elétrica. Ele adotou que prótons e nêutrons (no caso de bárions) bem como os píons (no caso de mésons) possuem estranheza nula. O interessante desta organização é que Gell-Mann, no caso de bárions mais pesados, conseguiu prever a existência de uma nova partícula, o . descoberta em 1964. Todos novas partículas, na década que se seguiu à proposta do Eighfold Way pode ser classificada neste esquema, o que tornou esta organização bastante aceita. Hoje sabe-se que esta é uma representação gráfica de um grupo de simetria utilizado em física de partículas.n
n
nn

nFigura 17 – Octeto para mésons.
n
n

nFigura 18 – Octeto para bárions.
n
n

nFigura 19 – Decupleto para bárions.n
n
nnNão demorou muito para o próprio Gell-Mann perceber que estas partículas poderiam ser explicadas em termos de combinações de outras partículas, mais fundamentais, que ele nomeou de quarks. Para explicar as partículas conhecidas seriam necessários três quarks (e seus respectivos antiquarks) que são: up (u, Q = 2/3, S = 0, spin = 1/2), down (d q = -1/3, S = 0, spin = 1/2) e strange (s, Q = -1/3, S = -1, spin = 1/2). Os antiquarks correspondentes possuem carga elétrica invertida. O nome desses quarks (up, down, strange) são comumente denominado sabores. Neste modelo, mésons seriam compostos de um par quark + antiquark e bárions seriam compostos de três quarks ou três antiquarks. Por exemplo:
n
nn
n
n
nn
n
nOu seja, é uma questão simples de combinatória descrever estas partículas em termos de quarks. Como necessário para qualquer hipótese, não basta explicar o que já existe, precisamos submeter estas hipóteses a testes e validações. Se quarks realmente existem, deveríamos ser capazes de observá-los. Assim como ionizamos um átomo, incidindo fótons energéticos sobre ele, deveríamos ser capazes de ionizar mésons e bárions (que, daqui para frente chamaremos genericamente de hádrons). E quarks deveriam ser fáceis de serem observados. Basta procurar por partículas com cargas elétricas fracionadas. De fato, experimentos similares ao de Millikan não foram capazes de medir nenhuma carga fracionária. Por exemplo, o grupo de Microdrop Particle Search, em Stanford, com um aparato com resolução para medir 1/24 da carga do elétron , já mediu cerca de 100 milhões de gotas e não obteve nenhuma evidência de cargas fracionárias. Uma solução para este problema, que ainda é um grande objeto de pesquisa, foi postular a propriedade de confinamento dos quarks, que diz que quarks são partículas que estão sempre confinadas em hádrons. Na verdade, isso é uma observação até a data atual, a menos em situações extremas de energia, onde há indícios de estados onde quarks estariam desconfinados, o plasma de quarks e glúons. Acontece que este estado, criado em laboratório nos aceleradores RHIC e LHC, possui vida média muito curta, da ordem de 10^-20 s, e o seu resfriamento faz com que quarks voltem a ficar confinados. Ou seja, até hoje não conseguimos isolar um quark em laboratório.
n
nMesmo estando confinados, temos algum acesso a suas propriedades. Um simples experimento, similar ao de Rutherford, pode indicar a presença de quarks no interior de hádrons. Isso foi feito no Stanford Linear Accelerator (SLAC) nos anos de 1960. Bombardeia-se prótons com feixes de elétrons de altas energias. Como quarks possuem carga elétrica, é possível haver interação entre elétrons e quarks e estes elétrons são espalhados. A seção de choque de espalhamento pode ser deduzida em termos da fração do momento do próton carregado por uma partícula no seu interior, nn. Se o próton for fundamental, a seção de choque será máxima para e nula para outros valores. Se o próton for constituído por três partículas fundamentais não interagentes entre si, a seção de choque será máxima para . A figura 20 explica graficamente estas possibilidades.n
n
nn

nFigura 20 – Expectativa para a seção de choque de espalhamento de elétrons por prótons para várias estruturas diferentes.
n
nnOs experimentos no SLAC mediram estas seções de choque (que hoje chamamos de PDF, do Inglês, Parton Distribution Funtion) e um resultado pode ser visto na figura 21. O termo parton é comumente utilizado para designar os constituintes de um hádron, de forma genérica. Um artigo de revisão interessante sobre os experimentos no SLAC e a descoberta dos quarks pode ser encontrado neste link.n
n
nn

nFigura 21 – Resultados do SLAC de espalhamento inelástico profundo.
n
nnApesar de o modelo de quarks conseguir explicar bem os hádrons, um novo problema surgiu. A partícula . esta partícula é composta de três quarks u em um estado de spin total 3/2. Isso significa que os três quarks deveriam estar no mesmo estado quântico. Como quarks são férmions (spin 1/2), o Princípio de Exclusão de Paulo proíbe essa combinação. Greenberg, em 1964, propôs uma solução para este problema. Ele propôs a existência de novos graus de liberdade, através de um novo número quântico, para os quarks: o número quântico de cor. Além dos três sabores de quarks, cada um deles poderiam vir também em três cores (vermelho, verde ou azul. O no Inglês, red, green, blue). Assim, com este grau de liberdade a mais o problema da partícula estaria resolvido, pois cada quark estaria em uma cor diferente, não violando o Princípio de Exclusão de Pauli. Antiquarks carregariam anticores. Três cores (ou três anticores) distintas formam um estado neutro de cor (branco), bem como um estado de cor + anticor correspondente (vermelho + antivermelho) também forma um estado neutro de cor. Gostaria de reforçar aqui que o termo cor é apenas uma representação. poderia ser 1,2,3; a,b,c; ou qualquer outra nomenclatura. O interessante da cor é esta visualização imaginativa que fazemos ao olhar os estados hadrônicos. Na verdade, a representação matemática desses estados são vetores de três dimensões, onde cada dimensão corresponde a uma cor diferente. Neste contexto, a matemática, além de elegante, torna-se fácil de compreender. Uma propriedade interessante nesta formalização é que:
n
nTodos os estados hadrônicos são neutros em cor.
n
nDe fato, nunca observamos nenhum estado hadrônico que não seja neutro em cor. Este fato empírico explica, por exemplo, porque observamos estados de três quarks (bárions), três antiquarks (antibárions) ou estados de um quark+antiquark (méson). Não observamos na natureza estados de dois quarks + antiquark, por exemplo, por ser impossível compor um estado neutro de cor com esta combinação. Há várias evidências experimentais da existência de graus de liberdade de cor e que o número de cores são 3. A primeira delas vem da razão entre as seções de choque de colisões elétron-pósitron para hádrons e seções de choque de colisões elétron-pósitron para múons. Esta razão é proporcional ao número de cores, por simples combinatória. Uma outra evidência importante vem da medida da largura de decaimento do píon neutro em dois fótons, . Esta largura de decaimento é proporcional ao número de cores ao quadrado e o valor experimental é 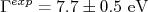. Para três cores o valor calculado seria enquanto que para apenas uma cor (ou não existência de cores) o valor calculado seria .
n
nComo é a interação entre quarks? O que dá origem à interação que mantém estas partículas confinadas em hádrons de forma tão extrema que torna-se impossível (até o momento) observar quarks livres? Analogamente ao fóton, responsável pela interação eletromagnética, glúons seriam os bósons mediadores da força forte a nível de quark. Ao contrário do fóton, que não possui carga elétrica, glúons possuem carga de cor e, por conta disso, podem interagir entre si. Esta possibilidade de interação entre glúons torna a força forte de curto alcance. Evidências da existência do glúon surgiram em 1978 do experimento PLUTO onde a observação de decaimentos em três jatos de partículas seriam devido a processos onde seriam produzidos três glúons (figura 22).
n
nn

nFigura 22 – Eventos de três jatos do experimento PLUTO indicando a existência de glúons.
n
nnNos anos seguintes ao modelo de quarks, entre os anos de 1970 e 2000, com o advento de novos aceleradores, novas evidências experimentais surgiram indicando a existência de três outros quarks, charm, bottom e top, além da existência de mais um outro lépton, o tau, e seus respectivos neutrinos.
n
nNo grande esquema das coisas, temos os quarks, léptons e os bósons mediadores das interações eletromagnéticas e forte. Falta ainda uma teoria, nos mesmos moldes, para o decaimento beta, a interação fraca. A teoria de Fermi para o decaimento beta, apesar de descrever bem os dados experimentais em baixas energias, falha no limite de altas energias. Além disso, ela não conta com um mediador da interação, como a eletromagnética e a forte. No modelo de Pauli, a natureza da interação fraca é de uma força de contato. De fato, o alcance da interação fraca é curtíssimo. Seguindo a ideia de Yukawa, esta interação deveria ser mediada por partículas extremamente massivas. Glashow, Weinberg e Salan desenvolveram, no final dos anos de 1960, uma teoria unificada para o eletromagnetismo e interação fraca. Nesta teoria, três bósons massivos seriam responsáveis pela interação fraca: os W⁺, W^– e Z⁰, com massas da orde de 80-90 GeV/c². Em 1983, o bóson W foi descoberto, seguido do bóson Z, alguns meses depois pela equipe liderada por Rubia e van der Meer nos experimentos UA1 e UA2 no CERN. No processo de unificação que culminou na teoria eletrofaca, a presença de quatro bósons, um sem massa, o fóton, e três extremamente massivos, é explicado pelo mecanismo de Higgs, cuja partícula, o bóson de Higgs, responsável pela massa das partículas fundamentais, foi descoberta recentemente no LHC, no CERN.n
n
nForam mais de um século de muitas evidências e desenvolvimentos experimentais e teóricos para culminar nas partículas fundamentais que representamos na figura 1. Com o advento do LHC, além da descoberta deste último pedaço no quebra-cabeças, o bóson de Higgs, muito ainda pode ser explorado e, quem sabe, novas evidências levem a caminhos que não prevíamos inicialmente.n
n
n

textos para leitura

n

n
1. Capítulo 1 do livro “Introduction to Elementary Particles”, D. Griffithsn
2. Capítulo 10 do livro “Nuclear and Particle Physics”, W. S. C. Williamsn
3. Capítulo 1 do livro “Quarks & Leptons”, F. Halzen e A. D. Martinn
4. Capítulo 6 do livro “Introdução à Física Nuclear e de Partículas Elementares”, Débora Menezesn

n
n
n

Exercícios

n

n
1. Considerando três quarks, up (u), down (d) e strange (s), faça as combinações possíveis de quarks-antiquarks para mésons e três quarks (ou três antiquarks) para bárions. Procure identificar cada uma destas combinações com o méson/bárion correspondente, olhando o site do Particle Data Group.n

]]>