Sistema de unidades

nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
nA física lida com grandezas de diferentes tipos e escalas de valores. Para representar numericamente estas grandezas é necessário definir sistemas de unidades, sendo o mais comum o MKSA (Metro-Kilograma-Segundo-Ampere). Este sistema é construído de forma a representar bem os valores típicos de grandezas na escala humana, onde o valor unitário de cada uma dessas grandezas é bem familiar (é fácil entender 1 kg ou 1 m). Acontece que a definição de algumas dessas escalas surgiu da comparação com padrões pré-estabelecidos (1 kg equivale à massa de 1 bloco de platina padrão no bureau de pesos e medidas). Isso gera inconvenientes, pois a unidade depende de fatores históricos e também de comparações com referências que podem estar sujeitas a flutuações e limitação em precisão. Além disso, grandezas em escalas muito diferentes do valor unitário da unidade tornam-se desconfortáveis de lidar, por exigirem potências de 10 ou muito grandes ou muito pequenas. Por exemplo, a massa do elétron no MKSA vale aproximadamente 9.1 x 10^-31 kg (note a potência de 10 elevado a -31). Assim, em fenômenos físicos onde a escala é muito diferente da unidade do sistema de medida as equações carregam enormes fatores de conversão. Por exemplo, no MKSA, a constante de Planck vale h = 6.62… x 10^-34 Js e todas as equações da Mecânica Quântica carregam esta constante de conversão de escala de alguma forma.
n
nPara resolver muitas das limitações decorrentes do uso de sistemas de unidades construídos a partir de eventos históricos e grandezas compatíveis com as escalas humanas, criou-se o sistema natural de unidades. Na verdade há vários desses sistemas, com pequenas variações dependendo do problema físico a ser abordado. O sistema natural de unidades tem por objetivo estabelecer como grandezas unitárias aquelas que tenham caráter físico universal, independentes da nossa vivência histórica. O metro, no MKSA, grandeza unitária para o comprimento, não tem este caráter. Além disso, pretende-se com o sistema natural de unidades estabelecer que estas grandezas não dependam de comparação com padrões pré-estabelecidos ou seja, estejam sujeitas a limitações nas suas precisões por conta de processos comparativos. Apesar desta vantagem, em geral não é possível realizar medidas em laboratório em unidades naturais, o que torna necessário realizar conversões que, via de regra, dependem do conhecimento experimental de uma grandeza fundamental (como a constante de Planck, por exemplo). Ou seja, a escolha de sistema natural de unidade não pressupõe a possibilidade de realizar medidas com precisão infinita. Outra característica importante do sistema natural de unidades é fazer com que equações para fenômenos físicos fundamentais sejam extremamente simplificadas, sem precisar de constantes de conversão de escalas exageradas. Propositadamente, sistemas naturais introduzem uma grande ambiguidade de unidades fazendo com que grandezas diferentes tenham, na prática, a mesma dimensão. Neste caso, é importante saber realizar análises dimensionais para poder converter, ao final de um problema, estas unidades para algo que seja simples de ser interpretado.
n
nComo dito, há várias variações de sistemas naturais de unidades. Elas se baseiam na escolha de constantes universais unitárias. Podemos citar, por exemplo:
n
nn

Unidades de Planck: $\hbar=c=G=k_B=1$ n
Unidades naturais de partículas: $\hbar=c=\epsilon_0=k_B=1$ n
Unidades de Stoney: n
Unidades atômicas: $e=m_e=\hbar=k_B=1$ n

n
nne por ai vai…
n
nUm detalhe importante em sistemas de unidades é o fato de que, constantes adimensionais não podem mudar de valor de um sistema para outro. Isso define fatores de escala e de conversão para as demais grandezas não unitárias do sistema. Além disso, é impossível criar sistemas de unidades onde dois observáveis diferentes, mas de mesma grandeza, tenham o mesmo valor. Por exemplo, é impossível criar um sistema de unidades onde a massa do próton e a massa do elétron sejam simultaneamente unitárias. Isto não tem sentido, uma vez que o próton possui massa muito maior que a do elétron.
n
nEm física de partículas elementares é comum utilizar o sistema de unidades no qual $\hbar=c=\epsilon_0=k_B=1$ . Já vi em livros pequenas variações deste sistema onde toma-se que $4\pi\epsilon_0=1$ , ao invés de $\epsilon_0=1$ . Vamos analisar como várias grandezas físicas são expressas neste sistema de unidades.n
n
nVamos olhar inicialmente a relação relativística entre massa, energia e momento. Para uma partícula relativística (vamos rever relatividade mais tarde), temos que:
n
n E^2=m^2c^4+p^2c^2

n
nTomando c=1

a relação acima fica muito mais simples, na forma:
n
n E^2=m^2+p^2

n
nO que nos leva a concluir que [E]=[m]=[p

], ou seja, energia, massa e momento têm a mesma unidade. Na física subatômica é comum utilizar como unidade para energia o elétron-volt [eV] e seus múltiplos, sendo bastante comuns o MeV e o GeV. Vamos olhar as relações de incerteza para estabelecer unidades para tempo e comprimento. Do princípio da incerteza para energia-tempo, temos que:n
n
n $\Delta E \Delta t \ge \hbar$ n
n
nTomando $\hbar=1$ , resulta, naturalmente que a unidade para o tempo é data pelo inverso da unidade de energia, ou seja, $[T]=[E]^{-1}$ . Se adotarmos para energia a escala de MeV, por exemplo, valores para o tempo seriam expressos em MeV^-1. É estranho falar em tempo com esta unidade mas é extremamente conveniente. Em breve isso ficará claro. Da mesma forma, podemos tomar a relação e incerteza para momento-posição, já tomando $\hbar=1$ :n
n
n $\Delta p \Delta x \ge 1$ n
n
nO que resulta que $[L]=[p]^{-1}$ . Como momento tem a mesma unidade de energia, posição tem a mesma unidade de tempo. No nosso exemplo, se momento for dado em MeV, posição será dada em MeV^-1. Note que sendo o tempo e posição expressos na mesma unidade, a descrição relativística da cinemática ficará extremamente mais simples, pois essas duas grandezas serão tratadas na mesma escala, sem a necessidade de fatores de conversão entre elas.
n
nNeste sistema de unidades, como a velocidade da luz é unitária e adimensional, qualquer velocidade também torna-se adimensional e $0 \le v \le 1$ . Da mesma forma, como $\hbar$ também é unitário e adimensional, grandezas expressas nesta constante também são adimensionais, como o momento angular.
n
nVamos agora olhar um pouco as constantes elétricas, já que comprimento, tempo e massa estão bem estabelecidas. Vamos tomar a definição da velocidade da luz no vácuo:n
n
n $c=\frac{1}{\sqrt{\epsilon_0 \mu_0}}$ n
n
nSabendo que, no nosso sistema de unidades, $c=\epsilon_0=1$ , consequentemente, $\mu_0=1$ , também sem dimensões. Tomando também a constante de estrutura fina:n
n
n $\alpha=\frac{e^2}{(4\pi\epsilon_0)\hbar c}\sim\frac{1}{137}$ n
n
nSendo $\alpha$ sem dimensão, o seu valor deve ser o mesmo independente do sistema de unidades. Isso faz com que, no nosso caso, o valor para a carga do elétron seja dado por:n
n
n $e=\sqrt{4\pi\alpha}\sim 0.303$ n
n
nE, consequentemente, carga elétrica, no sistema natural, seja também adimensional. Como corrente elétrica é definida com unidade tal que $[A]=[q][T]^{-1}$ , corrente elétrica possui a mesma unidade de energia.
n
nFinalmente, no sistema natural que adotamos, a constante de Boltzman k_B=1

faz com que $1=[E][Temp]^{-1}\rightarrow[Temp]=[E$ ], ou seja, temperatura e energia têm a mesma unidade.
n
nNote que, neste sistema, precisamos apenas de uma grandeza dimensional, a energia. Todas as outras grandezas têm unidade de energia ou de uma potência da energia. Isto simplifica demais qualquer conta que precisemos fazer, pois não precisamos nos preocupar em conversões de unidades. Por outro lado, não é fácil imaginar um intervalo de tempo em MeV^-1. A gente consegue quantificar tempo em múltiplos de segundo. Sendo assim, no final, quando necessitamos mostrar resultados finais de um cálculo, até mesmo para comparar com valores experimentais, torna-se necessário converter as grandezas do sistema natural para uma unidade mais corriqueira. Para isso, saber fazer análise dimensional é bastante importante. Vale lembrar então que:n
n
nn $\hbar = 1 = 6.582\times 10^{-22} \text{ MeV s} \rightarrow 1 \text{ MeV}^{-1} = 6.582 \times 10^{-22} \text{ s}$ nn
n
nOu ainda, utilizando a relação (mostre esta relação):n
n
nn $\hbar c = 1 = 197.3 \text{ MeV fm} \rightarrow 1 \text{ MeV}^{-1} = 197.3 \text{ fm}$ nn
n
nO que permite converter as unidades de comprimento e tempo para valores familiares, lembrando que $1 \text{ fm} = 10^{-15} \text{ m}$ .
n
n

Exemplo

nO comprimento de onda comptom para o píon, no sistema natural de unidades é:n
n
n $\lambda_{\pi} = \frac{\hbar}{m_{\pi}c} = \frac{1}{m_{\pi}} \sim 0.0071\text{ MeV}^{-1}$ nn
nUtilizando o nosso fator de conversão para fm, temos que:n
n
nn $\lambda_{\pi} \sim 0.0071 \times 197.3 \text{ fm} \sim 1.41 \text{ fm}$ nn
nTipicamente a seção de choque hadrônica é da ordem do quadrado do comprimento de onda comptom, ou seja:n
n
nn $\sigma\sim\lambda_{\pi}^2\sim 5\times 10^{-5} \text{ MeV}^{-2}$ nn
nQue, convertido para fm², resulta em:n
n
nn $\sigma\sim 5\times 10^{-5} \times (197.3)^2 \text{ fm}^{2} \sim 2 \text{ fm}^{2}$ nn
n

Leitura recomendada

http://en.wikipedia.org/wiki/Natural_unitsn

Exercícios

É comum utilizar, em física de partículas e física nuclear experimentais, a unidade de tempo . Obtenha o fator de escala para tempo no sistema natural de unidades e esta escala, normalmente adotada em física experimental.n
A fórmula de Gell-Mann/Okubo de massa relaciona as massas das partículas no octeto de bárions (supondo massa do próton e nêutron iguais), bem como das partículas $\Sigma^0,\Sigma^+,\Sigma^-$ iguais entre si e $\Xi^0,\Xi^-$ , também iguais, através da relação
n
n $2(m_p+m_\Xi) = 3m_\Lambda + m_\Sigma$
n
nCalcule, utilizando as massas no Particle Data Group, a massa da partícula $\Lambda$ . Compare com o valor tabelado.n
Calcule, a partir dos valores tabelados no Particle Data Group, a vida média do múon 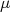$\mu$ e do taú $\tau$ no sistema natural de unidades. n
Calcule o valor de momento $|\vec p| = 1\text{ GeV}$ no MKSA.n
Obtenha as unidades de força, pressão, campo elétrico e campo magnético no sistema natural de unidades. Obtenha os fatores de conversão para o MKSA destas unidades.n
Qual a temperatura em graus Celsius de um sistema a uma temperatura de 150 MeV?n

]]>

Exemplo

Leitura recomendada

Exercícios

Deixe um comentário Cancelar resposta