nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
nn
nEstudos experimentais em física de partículas são realizados, como dito anteriormente, principalmente através do estudo de decaimentos de partículas instáveis e de reações entre partículas. Vamos estudar um pouco esses dois processos. Antes disso, precisamos compreender um pouco alguns aspectos das colisões entre partículas relativísticas.
n
nEm colisões clássicas, supondo o sistema não sujeito à ações de forças externas, momento e massa são sempre conservados enquanto a conservação da energia depende do tipo de colisão que estamos estudando. Em colisões relativísticas, não sujeitas a ações de forças externas, a situação é diferente. Há também a conservação de momento. Porém, neste caso, energia é sempre conservada. O que não precisa ser conservado, neste caso é a energia cinética do sistema estudado. Colisões relativísticas são classificadas em três tipos:n
n
n
- n
- Elástica: energia cinética é conservada;n
- Inelástica: energia cinética final é menor que a inicial;n
- Explosiva: energia cinética final é maior que a inicial;n
nVocê deve estar se perguntando: se a energia é sempre conservada e a energia cinética, não necessariamente, o que acontece? O que ocorre, em colisões relativísticas é a conversão entre energia cinética em energia de repouso do sistema e vice versa. Por conta disso, em colisões relativísticas, a massa não é necessariamente conservada. Isso fica óbvio, por exemplo, na reação de aniquilação elétron-pósitron,
 , onde toda a massa inicial do sistema é convertida em energia cinética para os dois fótons resultantes. Neste caso, esta é uma reação explosiva. Nos casos clássicos equivalentes (por exemplo, a explosão de uma granada), nós atribuímos o aumento da energia cinética à uma “energia interna” do sistema que seria liberada, mas nós não nos preocupamos muito com isso e, sabendo o quanto de energia é liberada, nós sabemos resolver o problema proposto. O oposto também é válido. Relativisticamente, a reação de produção de pares,
, onde toda a massa inicial do sistema é convertida em energia cinética para os dois fótons resultantes. Neste caso, esta é uma reação explosiva. Nos casos clássicos equivalentes (por exemplo, a explosão de uma granada), nós atribuímos o aumento da energia cinética à uma “energia interna” do sistema que seria liberada, mas nós não nos preocupamos muito com isso e, sabendo o quanto de energia é liberada, nós sabemos resolver o problema proposto. O oposto também é válido. Relativisticamente, a reação de produção de pares,  , diminui a energia cinética final, por conta do aumento da energia de repouso do sistema (neste caso, na massa das partículas finais). No caso clássico nós culpamos a inelasticidade à perdas que podem ocorrer no sistema. Então é natural interpretar que, em colisões explosivas há uma diminuição da massa do sistema e, em colisões inelásticas, aumento da massa. Em colisões elásticas a massa se conserva.
, diminui a energia cinética final, por conta do aumento da energia de repouso do sistema (neste caso, na massa das partículas finais). No caso clássico nós culpamos a inelasticidade à perdas que podem ocorrer no sistema. Então é natural interpretar que, em colisões explosivas há uma diminuição da massa do sistema e, em colisões inelásticas, aumento da massa. Em colisões elásticas a massa se conserva.n
nPor conta dessas características, colisões relativísticas podem ser tratadas através de uma simples relação de igualdade entre quadrimomentos antes e após a colisão, na forma:nn
n
 |
n
n
n
Decaimentos em duas partículas
nEste é talvez o caso mais simples. A reação que estamos estudando, no caso de decaimento de duas partículas é:nnn
 |
n
n
 e
e  , criando dois vínculos e diminuindo para 6 o número de grandezas independentes. Ademais, requerendo a conservação do quadrimomento:nn
, criando dois vínculos e diminuindo para 6 o número de grandezas independentes. Ademais, requerendo a conservação do quadrimomento:nnn
 |
n
n
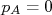 , ou seja, no referencial do centro de momentos do sistema. Neste caso, por conta da igualdade entre quadrimomentos, vê-se que
, ou seja, no referencial do centro de momentos do sistema. Neste caso, por conta da igualdade entre quadrimomentos, vê-se que  , isto é, as partículas são emitidas com mesmo momento, em sentidos opostos. Sabendo-se o ângulo de emissão de uma delas, conhece-se o ângulo de emissão da outra. No referencial de repouso da partícula A, seu quadrimomento vale
, isto é, as partículas são emitidas com mesmo momento, em sentidos opostos. Sabendo-se o ângulo de emissão de uma delas, conhece-se o ângulo de emissão da outra. No referencial de repouso da partícula A, seu quadrimomento vale  . Neste caso:nn
. Neste caso:nnn
 |
n
n
n
 |
n
n
n
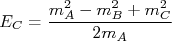 |
n
n
n
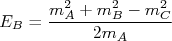 |
n
n
 e encontrar o momento de cada uma delas.
e encontrar o momento de cada uma delas.n
n
Exemplos
nVamos tomar o decaimento . Sabemos que
. Sabemos que  e a massa do fóton é nula. Assim, podemos calcular que:nn
e a massa do fóton é nula. Assim, podemos calcular que:nnn
 |
n
n
n
nVamos agora olhar um segundo exemplo, o decaimento do píon positivo,
 , onde
, onde 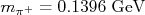 ,
,  e o neutrino tem massa nula. É fácil calcular, neste caso, que as energias de cada partícula são:nn
e o neutrino tem massa nula. É fácil calcular, neste caso, que as energias de cada partícula são:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
n
Saindo do centro de momentos
nNo caso de a partícula A não estar no repouso (outro referencial que não seja no laboratório) o cálculo das energias e momentos das partículas B e C pode ser feito considerando o decaimento no centro de momentos e fazendo a transformação de Lorentz correspondente para o referencial do laboratório. A situação está esquematizada na figura 1.nn
n

nFigura 1 – Decaimento em duas partículas.
n
n
 da partícula B e sabendo também que o decaimento ocorre em um plano, portanto escolhendo x para o eixo perpendicular à z, podemos escrever que as componentes dos momentos, neste referencial, são:nn
da partícula B e sabendo também que o decaimento ocorre em um plano, portanto escolhendo x para o eixo perpendicular à z, podemos escrever que as componentes dos momentos, neste referencial, são:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
n
 |
n
n
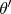 no referencial do laboratório através da relação de momentos no referencial do laboratório:nn
no referencial do laboratório através da relação de momentos no referencial do laboratório:nnn
 |
n
n
Colisões relativísticas
nEm colisões relativísticas, geralmente tratamos de uma colisão do tipo . Este caso geral pode, com algum trabalho, ser bem descrito por um sistema do tipo
. Este caso geral pode, com algum trabalho, ser bem descrito por um sistema do tipo  , duas partículas colidindo e gerando, após a colisão, outras duas, que podem ou não serem iguais às iniciais. Do ponto de vista experimental, a região de interação entre elas é inacessível e, o experimento mede as grandezas assintóticas dessas partículas, quando elas não mais interagem entre si. Historicamente, estes experimentos consistiam de um feixe de partículas incidindo sobre um alvo parado no referencial do laboratório. Sendo a partícula B o alvo, isto significaria que
, duas partículas colidindo e gerando, após a colisão, outras duas, que podem ou não serem iguais às iniciais. Do ponto de vista experimental, a região de interação entre elas é inacessível e, o experimento mede as grandezas assintóticas dessas partículas, quando elas não mais interagem entre si. Historicamente, estes experimentos consistiam de um feixe de partículas incidindo sobre um alvo parado no referencial do laboratório. Sendo a partícula B o alvo, isto significaria que 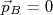 . Hoje em dia, em aceleradores modernos, ou colisores, ambas as partículas são aceleradas de tal forma que o referencial do laboratório coincide com o referencial do centro de momento das colisões, tornando o tratamento ainda mais simples. Sendo assim, vamos inicialmente tratar o problema neste referencial.n
. Hoje em dia, em aceleradores modernos, ou colisores, ambas as partículas são aceleradas de tal forma que o referencial do laboratório coincide com o referencial do centro de momento das colisões, tornando o tratamento ainda mais simples. Sendo assim, vamos inicialmente tratar o problema neste referencial.nn
nPara caracterizar uma colisão deste tipo, precisamos definir variáveis como energia, momento e ângulo de espalhamento. Do ponto de vista relativístico, estas grandezas podem ser representadas pelas variáveis de Mandelstam, definidas como:nn
n
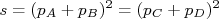 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
 está relacionada à energia da colisão no centro de momentos. É por conta disso que muitos artigos, trabalhos em conferências, etc. apresentam resultados de experimentos para um dado valor de
está relacionada à energia da colisão no centro de momentos. É por conta disso que muitos artigos, trabalhos em conferências, etc. apresentam resultados de experimentos para um dado valor de  . As variáveis
. As variáveis  e
e 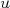 estão relacionadas aos ângulos de espalhamento e transferência de momento das partículas iniciais para as finais, através de:nn
estão relacionadas aos ângulos de espalhamento e transferência de momento das partículas iniciais para as finais, através de:nnn
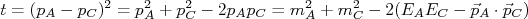 |
n
n
n
 |
n
n
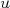 .n
.n
Rapidez e pseudo-rapidez
nEm colisões entre partículas a situação cinemática de cada uma delas é definida pelas medidas de momentos e ângulos de emissão. Há o inconveniente de que a transformação entre referenciais para ângulos não ser muito simples, o que acarreta em uma algebra um pouco mais trabalhosa. Minkowski percebeu que poderíamos tratar transformações de Lorentz como rotações hiperbólicas e isso poderia simplificar significativamente a interpretação de ângulos de emissão e mudanças de referenciais. Vamos tomar, por exemplo, um boost na direção z. As transformações de Lorentz para momento e energia são (de forma similar para tempo e posição):nnn
 |
n
n
n
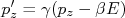 |
n
n
n
 |
n
n
 , que é uma equação hiperbólica, descrita por
, que é uma equação hiperbólica, descrita por  . Isto é, as transformações acima podem ser escritas como uma rotação hiperbólica neste ângulo de modo que:nn
. Isto é, as transformações acima podem ser escritas como uma rotação hiperbólica neste ângulo de modo que:nnn
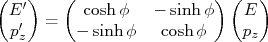 |
n
n
 como o de repouso da partícula, ou seja,
como o de repouso da partícula, ou seja,  e
e  , podemos escrever que:nn
, podemos escrever que:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
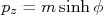 |
n
n
n
n
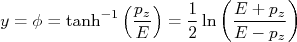 n
nn
n
 é denominada de rapidez da partícula no referencial do laboratório. Esta grandeza é bastante utilizada em física de partículas por conta da simplicidade que é realizar mudanças de referenciais. A rapidez não é invariante por transformações de Lorentz, ela assume um valor diferente para cada referencial. Contudo, uma mudança do referencial 1 para o referencial 2 da rapidez de uma partícula consiste simplesmente na soma ou subtração de uma constante. Se uma partícula, no referencial
é denominada de rapidez da partícula no referencial do laboratório. Esta grandeza é bastante utilizada em física de partículas por conta da simplicidade que é realizar mudanças de referenciais. A rapidez não é invariante por transformações de Lorentz, ela assume um valor diferente para cada referencial. Contudo, uma mudança do referencial 1 para o referencial 2 da rapidez de uma partícula consiste simplesmente na soma ou subtração de uma constante. Se uma partícula, no referencial  move-se com rapidez
move-se com rapidez  , a rapidez desta partícula no referencial
, a rapidez desta partícula no referencial  , que se move em relação à
, que se move em relação à  com velocidade
com velocidade  é dada por:nn
é dada por:nnn
 |
n
n
n
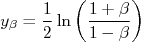 |
n
n
 é chamada de rapidez do referencial
é chamada de rapidez do referencial  em relação ao referencial
em relação ao referencial  . Ou seja, mudanças de referenciais se tornam extremamente simples.n
. Ou seja, mudanças de referenciais se tornam extremamente simples.nn
nEm muitas situações experimentais não é possível medir a energia das partículas, apenas o seu momento. Por exemplo, em um detector de trajetória inserido em um campo magnético, onde se registra apenas a curvatura da trajetória da partícula, mede-se apenas o seu momento (e carga, dependendo do sinal da curvatura). Assim, não é possível identificar a partícula e, consequentemente, medir a sua energia. Medindo o momento da partícula, pode-se saber o ângulo no qual ela foi espalhada. Nestes casos não é possível medir a rapidez desta partícula. Define-se a pseudo-rapidez da partícula como sendo:nn
n
 |
n
n
 e, neste caso, a pseudo-rapidez coincide com a rapidez.nn
e, neste caso, a pseudo-rapidez coincide com a rapidez.nn
Leitura recomendada
n- n
- Capítulo 3 do livro “Introduction to Elementary Particles”, D. griffithsn
- Capítulo 1 do livro “Particle Physics, an introduction”, M. Leon (note que ele utiliza um formalismo ligeiramente diferente para representação das transformações de Lorentz, mas vale a pena conhecer.).n
- Capítulo 1 do livro “Introduction to high-energy heavy-ion collisions”, Cheuk-Yin Wong.n
- Na aula comentamos o decaimento de três corpos e o gráfico de Dalitz. Para uma discussão da cinemática de um decaimento de três corpos e o gráfico de Dalitz, dêem uma olhada neste review de cinemática relativística do Particle Data Group.n
Exercícios
n- n
- Uma partícula
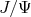 de momento 10 GeV decai em elétron + pósitron. No referencial do centro de massa desta partícula o elétron foi emitido a 45o em relação ao que seria a direção do momento do
de momento 10 GeV decai em elétron + pósitron. No referencial do centro de massa desta partícula o elétron foi emitido a 45o em relação ao que seria a direção do momento do 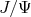 no laboratório. Calcule, no referencial do laboratório, o ângulo entre o elétron e pósitron, bem como as energias destas partículas.n
no laboratório. Calcule, no referencial do laboratório, o ângulo entre o elétron e pósitron, bem como as energias destas partículas.n
- Em um decaimento de três corpos,
 , determine a energia máxima e mínima da partícula B em termos das massas das demais partículas.n
, determine a energia máxima e mínima da partícula B em termos das massas das demais partículas.n
- Mostre a equação (21).n
- Mostre que uma partícula movendo-se na direção z com velocidade
 possui rapidez dada pela eq. (34)n
possui rapidez dada pela eq. (34)n
- Mostre a equação (33).n
- Mostre a equação (35).n
- Mostre que no limite de altas energias, onde a massa de repouso da partícula pode ser desprezada, que a pseudo-rapidez converge para a rapidez da partícula.n
- Mostre que rapidez, no limite de baixas velocidades,
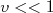 , tende a se igualar à velocidade da partícula.n
, tende a se igualar à velocidade da partícula.n
- Para uma colisão elástica entre partículas idênticas,
 , mostre que as variáveis de Mandelstan tornam-se
n
, mostre que as variáveis de Mandelstan tornam-se
n
n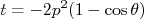
n nonde
nonde  corresponde ao momento da partícula incidente no referencial do CM e
corresponde ao momento da partícula incidente no referencial do CM e  é o ângulo da partícula espalhada.nn
é o ângulo da partícula espalhada.nn
Deixe um comentário