nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
nn
nNa aula passada introduzimos alguns números quânticos que são utilizados para caracterizar reações envolvendo partículas. Na maioria dos casos estes números quânticos são conservados porém, principalmente em interações fracas e eletromagnéticas, alguns desses números quânticos não se conservam. A dependência do processo físico para decidir se há ou não conservação de números quânticos deve estar presente em alguma característica fundamental das interações que regem estes processos. Por conta disso, entender os princípios que estabelecem a conservação ou não de propriedades físicas de um sistema é um passo importante no aprendizado das interações fundamentais. Vamos ver que a conservação de uma grandeza física está intimamente ligada a uma invariância por uma transformação qualquer do sistema, isto é, uma simetria apresentada pelo sistema. No início do séc. XX, Emmy Noether publicou um teorema, que leva seu nome, que relacionava a presença de uma simetria em um sistema físico a uma lei de conservação. Para cada simetria presente no sistema há uma lei de conservação. Do ponto de vista experimental, o inverso é mais apropriado: para cada lei de conservação deve haver uma simetria no sistema físico. Isto é interessante porque a observação de fenômenos resultam na observação dessas leis de conservação, que guiam o caminho dos pesquisadores para tentar explicar fundamentalmente as interações respeitando as devidas simetrias. Por exemplo, a conservação de diversos números quânticos em interações fortes estabelecem condições de contorno nas teorias formuladas para estas interações. Vamos ver que há uma representação bastante útil para representar estas simetrias, através de teoria de grupos, um ramo da matemática fundamental para o estudo de simetrias.n
n
nAlgumas das simetrias mais fundamentais estão listadas na tabela 1, abaixo. n
n
n
n
|
|
|
|
|
|
|
|
|
n
nTomemos como exemplo a translação espacial. Imagine um sistema de 2 partículas sujeitas a uma força conservativa que dependa apenas da distância entre elas. Neste caso, poderíamos escrever que o potencial de interação é, em um sistema de coordenadas qualquer:n
n
n

n
nFaçamos agora uma translação no sistema de coordenadas, ou seja:nn
n
 |
n
n
n
 |
n
n
n
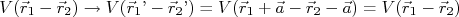 |
n
n
n
 |
n
n
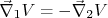 , por conta da diferença
, por conta da diferença  , resulta que a força total é nula e, neste caso:nn
, resulta que a força total é nula e, neste caso:nnn
 |
n
n
 , sendo
, sendo  a energia cinética e
a energia cinética e  , a energia potencial.
, a energia potencial.  são, respectivamente, as velocidades e posições generalizadas. As equações do movimento podem ser escritas resolvendo as equações:nn
são, respectivamente, as velocidades e posições generalizadas. As equações do movimento podem ser escritas resolvendo as equações:nnn
 |
n
n
 como sendo:nn
como sendo:nnn
 |
n
n
n
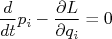 |
n
n
 , o momento associado a esta coordenada será uma constante do sistema, ou seja, é uma grandeza conservada. Isto é equivalente a dizer que uma transformação do tipo:nn
, o momento associado a esta coordenada será uma constante do sistema, ou seja, é uma grandeza conservada. Isto é equivalente a dizer que uma transformação do tipo:nnn
 |
n
n
 , a posição do centro de momentos e
, a posição do centro de momentos e  , a posição relativa entre as partículas 1 e 2, pode-se mostrar que a lagrangeana resultante não depende explicitamente de
, a posição relativa entre as partículas 1 e 2, pode-se mostrar que a lagrangeana resultante não depende explicitamente de  e, consequentemente, seu momento associado, neste caso, o momento total, é conservado. n
e, consequentemente, seu momento associado, neste caso, o momento total, é conservado. nn
nPrecisamos transportar esses conhecimentos acerca de simetrias para o mundo quântico. Apesar de o formalismo lagrangeano ser mais apropriado para tratar sistemas quânticos relativísticos, vamos olhar a questão de constantes de movimento e simetrias usando o formalismo hamiltoniano, que é mais familiar aqueles que têm apenas cursos introdutórios de mecânica quântica.
n
nUma grandeza física qualquer pode ser obtida através do valor esperado do seu operador em relação ao estado quântico estudado, ou seja:nn
n
 |
n
n
n
 |
n
n
n
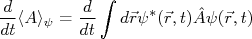 |
n
n
n
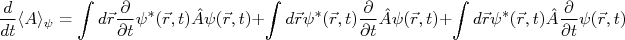 |
n
n
n
 |
n
n
n
 |
n
n
 é hermitiano, podemos rescrever a primeira integral e, reorganizando as integrais acima, temos:nn
é hermitiano, podemos rescrever a primeira integral e, reorganizando as integrais acima, temos:nnn
 |
n
n
n
![\frac{d}{dt} \langle A \rangle_{\psi} = \langle \frac{\partial}{\partial t}\hat A \rangle_{\psi} + i \langle [\hat H,\hat A] \rangle_{\psi} \frac{d}{dt} \langle A \rangle_{\psi} = \langle \frac{\partial}{\partial t}\hat A \rangle_{\psi} + i \langle [\hat H,\hat A] \rangle_{\psi}](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/b46996c517256ce5a0a88a11fc1dca4e.png) |
n
n
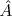 não dependa explicitamente do tempo e caso
não dependa explicitamente do tempo e caso ![[\hat H,\hat A]=0 [\hat H,\hat A]=0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/b870cfc751ba215141e286fae074de54.png) , então o valor médio de
, então o valor médio de  é constante. Nesse caso, podemos dizer que essa grandeza é uma constante do movimento. Essa igualdade é particularmente importante pois permite obter claramente quais são as constantes de movimento de um sistema quântico. n
nUm aspecto interessante da equação (17) é a consequência que, se houver estados quânticos que sejam, simultaneamente, auto-estados de um operador
é constante. Nesse caso, podemos dizer que essa grandeza é uma constante do movimento. Essa igualdade é particularmente importante pois permite obter claramente quais são as constantes de movimento de um sistema quântico. n
nUm aspecto interessante da equação (17) é a consequência que, se houver estados quânticos que sejam, simultaneamente, auto-estados de um operador  e da Hamiltoniana do sistema, a grandeza
e da Hamiltoniana do sistema, a grandeza  será uma constante do movimento. Para mostrar isso, basta aplicar o comutador desse operador e da Hamiltoniana nesses auto-estados, supondo
será uma constante do movimento. Para mostrar isso, basta aplicar o comutador desse operador e da Hamiltoniana nesses auto-estados, supondo 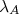 e
e  auto-valores de
auto-valores de 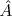 e
e  , respectivamente:nn
, respectivamente:nnn
![[\hat H,\hat A]|\psi\rangle = (\hat H\hat A - \hat A\hat H)|\psi\rangle = \hat H\hat A|\psi\rangle - \hat A\hat H|\psi\rangle = \hat H\lambda_A|\psi\rangle - \hat A\lambda_H|\psi\rangle [\hat H,\hat A]|\psi\rangle = (\hat H\hat A - \hat A\hat H)|\psi\rangle = \hat H\hat A|\psi\rangle - \hat A\hat H|\psi\rangle = \hat H\lambda_A|\psi\rangle - \hat A\lambda_H|\psi\rangle](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/45f9be8305d638ef8f3eddf029770029.png) |
n
n
n
![[\hat H,\hat A]|\psi\rangle = \lambda_A\hat H|\psi\rangle - \lambda_H\hat A|\psi\rangle = \lambda_A\lambda_H|\psi\rangle - \lambda_H\lambda_A|\psi\rangle = 0 [\hat H,\hat A]|\psi\rangle = \lambda_A\hat H|\psi\rangle - \lambda_H\hat A|\psi\rangle = \lambda_A\lambda_H|\psi\rangle - \lambda_H\lambda_A|\psi\rangle = 0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/10f47135ddedb234232d9dcd3483c8ed.png) |
n
n
n
![[\hat H,\hat A]|\psi\rangle = 0 \rightarrow [\hat H,\hat A] = 0 [\hat H,\hat A]|\psi\rangle = 0 \rightarrow [\hat H,\hat A] = 0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/949df32287e072b88deb2f9b0eda0b30.png) |
n
n
n
nVamos tentar construir operadores que realizem uma transformação no sistema, seja ela de rotação, deslocamento espacial ou temporal, ou outra transformação qualquer. Vamos fazer isso olhando exemplos simples e dai, tentar retirar uma forma para estas operações de transformação. Vamos começar por uma transformação temporal. A evolução temporal de um estado quântico pode ser escrita através de:nn
n
 |
n
n
n
 |
n
n
n
 |
n
n
 realiza uma transformação temporal do tipo
realiza uma transformação temporal do tipo  no estado quântico do sistema.
no estado quântico do sistema.n
nVamos usar esta mesma estrutura para tentar construir um operador similar para uma transformação espacial. Considere agora o estado
 , autoestado do operador
, autoestado do operador  com autovalor
com autovalor  . Deste modo, podemos escrever que:nn
. Deste modo, podemos escrever que:nnn
 |
n
n
n
 |
n
n
 . Qual o valor esperado do operador
. Qual o valor esperado do operador  para este estado? Precisamos calcular, então, a grandeza:nn
para este estado? Precisamos calcular, então, a grandeza:nnn
 |
n
n
n
 |
n
n
 em uma série de Taylor em torno de
em uma série de Taylor em torno de  , temos que:nn
, temos que:nnn
 |
n
n
 . O segundo termo (
. O segundo termo ( ) vale:nn
) vale:nnn
 |
n
n
n
 |
n
n
n
![\hat Y^1 &= (-\hat B\hat A +\hat A \hat B)s = [\hat A,\hat B]s \hat Y^1 &= (-\hat B\hat A +\hat A \hat B)s = [\hat A,\hat B]s](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/a131fd5bfaa6cbd18c96b377226ec6b1.png) |
n
n
 pode ser calculado da mesma maneira e é fácil mostrar que:nn
pode ser calculado da mesma maneira e é fácil mostrar que:nnn
![\hat Y^2 = \frac{1}{2!}[ [\hat A,\hat B],\hat B] s^2 \hat Y^2 = \frac{1}{2!}[ [\hat A,\hat B],\hat B] s^2](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/bf98dd9e9cca7a6a29bcddc944e39e34.png) |
n
n
 ) por:nn
) por:nnn
![\exp(-\hat B)\hat A\exp(\hat B) = \hat A + [\hat A,\hat B] +\frac{1}{2!}[ [\hat A,\hat B],\hat B] + ... \exp(-\hat B)\hat A\exp(\hat B) = \hat A + [\hat A,\hat B] +\frac{1}{2!}[ [\hat A,\hat B],\hat B] + ...](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/d1aa6088a73301920be658c3653be2c1.png) |
n
n
![[\hat x,\hat p_x] [\hat x,\hat p_x]](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/e397701505dfacade3a406574d580084.png) é um número, o que anula todos os termos subsequentes. Assim, sabendo que
é um número, o que anula todos os termos subsequentes. Assim, sabendo que ![[\hat x, \hat p_x]=i [\hat x, \hat p_x]=i](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/d80c982f1fa96cce4c97fe5e047f4a9b.png) , resolvendo (26) obtemos:nn
, resolvendo (26) obtemos:nnn
![\langle ?|\hat x|?\rangle = \langle x| \hat x + (-i\Delta x)[\hat x,\hat p_x]|x\rangle \langle ?|\hat x|?\rangle = \langle x| \hat x + (-i\Delta x)[\hat x,\hat p_x]|x\rangle](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/0379af85b06fd3829763a21b87d0311b.png) |
n
n
n
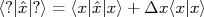 |
n
n
n
 |
n
n
 também é um autoestado do operador
também é um autoestado do operador  , com autovalor
, com autovalor 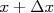 , o que nos permite concluir que o operador
, o que nos permite concluir que o operador 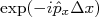 é responsável por uma translação espacial do sistema em
é responsável por uma translação espacial do sistema em  , ou seja, de forma similar à translação temporal:nn
, ou seja, de forma similar à translação temporal:nnn
 |
n
n
n
 |
n
n
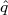 é um operador hermitiano e
é um operador hermitiano e  é a amplitude da transformação, que é uma quantidade real. O operador
é a amplitude da transformação, que é uma quantidade real. O operador  é unitário, ou seja,
é unitário, ou seja, 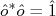 e, por conta disso não alterna as normalizações e produtos internos de estados quânticos. De fato, transformações em mecânica quântica são, na grande maioria, descritas por operadores unitários nesta forma. Uma exceção é a operação de reversão temporal, onde o operador é anti-unitário.
e, por conta disso não alterna as normalizações e produtos internos de estados quânticos. De fato, transformações em mecânica quântica são, na grande maioria, descritas por operadores unitários nesta forma. Uma exceção é a operação de reversão temporal, onde o operador é anti-unitário.n
nTemos dois ingredientes na mão. A condição para uma grandeza ser conservada em mecânica quântica é que o seu operador comute com a hamiltoniana do sistema e não dependa explicitamente do tempo. E que uma transformação em um sistema pode ser conduzida por um operador unitário como o descrito em (38). Precisamos agora conectar estes dois pedaços de informação e mostrar que uma transformação em um sistema evidencia uma simetria se o gerador desta transformação, o operador
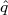 em (38), representar uma grandeza que é conservada. Para isto, vamos imaginar que uma transformação
em (38), representar uma grandeza que é conservada. Para isto, vamos imaginar que uma transformação  pode ser tratada como uma sucessão de infinitas transformações infinitesimais, ou seja, podemos utilizar a relação:nn
pode ser tratada como uma sucessão de infinitas transformações infinitesimais, ou seja, podemos utilizar a relação:nnn
 |
n
n
n
 |
n
n
 , podemos tomar apenas os dois primeiros termos na expansão em Taylor de (40) e escrever o operador como sendo:nn
, podemos tomar apenas os dois primeiros termos na expansão em Taylor de (40) e escrever o operador como sendo:nnn
 |
n
n
n
 =\langle a+\delta a|\hat H|a+\delta a\rangle’ alt=’< H > = \langle a|\hat H|a\rangle \rightarrow =\langle a+\delta a|\hat H|a+\delta a\rangle’ alt=’< H > = \langle a|\hat H|a\rangle \rightarrow |
n
n
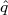 é hermitiano:nn
é hermitiano:nnn
 =\langle a+\delta a|\hat H|a+\delta a\rangle = \langle a|(1-i\hat q\delta a)^* \hat H (1-i\hat q\delta a)|a\rangle’ alt=’ =\langle a+\delta a|\hat H|a+\delta a\rangle = \langle a|(1-i\hat q\delta a)^* \hat H (1-i\hat q\delta a)|a\rangle’ alt=’ |
n
n
n
 = \langle a|(1+i\hat q^*\delta a) \hat H (1-i\hat q\delta a)|a\rangle’ alt=’ = \langle a|(1+i\hat q^*\delta a) \hat H (1-i\hat q\delta a)|a\rangle’ alt=’ |
n
n
n
 = \langle a| \hat H |a\rangle + i\delta a( \langle a|\hat q\hat H|a\rangle – \langle a|\hat H\hat q|a\rangle) + \mathcal{O}(\delta a^2)’ alt=’ = \langle a| \hat H |a\rangle + i\delta a( \langle a|\hat q\hat H|a\rangle – \langle a|\hat H\hat q|a\rangle) + \mathcal{O}(\delta a^2)’ alt=’ |
n
n
n
 = < H > + i\delta a \langle a|[\hat q,\hat H]|a\rangle + \mathcal{O}(\delta a^2)’ alt=’ = < H > + i\delta a \langle a|[\hat q,\hat H]|a\rangle + \mathcal{O}(\delta a^2)’ alt=’ |
n
n
![[\hat q,\hat H]=0 [\hat q,\hat H]=0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/c30af7a1f3f91398b619c83c8505372c.png) , em uma transformação infinitesimal,
, em uma transformação infinitesimal,  = < H > + \mathcal{O}(\delta a^2)’ alt=’< H > \rightarrow
= < H > + \mathcal{O}(\delta a^2)’ alt=’< H > \rightarrow 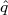 , evidenciando uma simetria no sistema por esta transformação. Isso implica, como vimos, que
, evidenciando uma simetria no sistema por esta transformação. Isso implica, como vimos, que  , que pode ser tão pequeno quanto queiramos. Situações como estas são classificadas como transformações contínuas. Porém, nem todas as transformações são contínuas, algumas delas (por exemplo, a paridade) não podem ser descritas como uma série de transformações infinitesimais e são normalmente chamadas de transformações discretas. Vamos tratar desse tipo de transformação em breve.n
, que pode ser tão pequeno quanto queiramos. Situações como estas são classificadas como transformações contínuas. Porém, nem todas as transformações são contínuas, algumas delas (por exemplo, a paridade) não podem ser descritas como uma série de transformações infinitesimais e são normalmente chamadas de transformações discretas. Vamos tratar desse tipo de transformação em breve.nn
nnVamos agora considerar a seguinte situação: imagine um sistema físico qualquer que possa ser representado pela Eq. de Schrödinger, abaixo:nn
n
 |
n
n
n
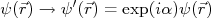 |
n
n
 é uma constante qualquer. Claramente esta transformação, uma simples mudança de fase, mantém (47) invariante. Esta transformação se aplica igualmente em todos os pontos espaciais-temporais e, como vimos, uma transformação deste tipo, quando mantém o sistema invariante, está relacionada a conservação de um número quântico do sistema. Transformações deste tipo, que são aplicadas igualmente em todo o espaço-tempo, são chamadas de transformações globais.
é uma constante qualquer. Claramente esta transformação, uma simples mudança de fase, mantém (47) invariante. Esta transformação se aplica igualmente em todos os pontos espaciais-temporais e, como vimos, uma transformação deste tipo, quando mantém o sistema invariante, está relacionada a conservação de um número quântico do sistema. Transformações deste tipo, que são aplicadas igualmente em todo o espaço-tempo, são chamadas de transformações globais.n
nPor outro lado, se a amplitude da transformação depender das coordenadas espaço-temporais, isto é, sua magnitude depender de cada ponto do espaço, a transformação é denominada de local. Seja, por exemplo, a transformação:nn
n
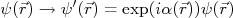 |
n
n
n
 |
n
n
 com as coordenadas espaciais, (47) não mantém a simetria do sistema. Neste caso dizemos que a Eq. de Schrödinger não mantém a simetria por uma transformação de fase local. Para tornar o sistema simétrico por transformações locais é necessário introduzir, deliberadamente, forças reais no problema. Neste problema especial, isto pode ser feito modificando, à mão, o operador gradiente de tal forma que:nn
com as coordenadas espaciais, (47) não mantém a simetria do sistema. Neste caso dizemos que a Eq. de Schrödinger não mantém a simetria por uma transformação de fase local. Para tornar o sistema simétrico por transformações locais é necessário introduzir, deliberadamente, forças reais no problema. Neste problema especial, isto pode ser feito modificando, à mão, o operador gradiente de tal forma que:nnn
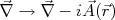 |
n
n
 se transforme na forma:nn
se transforme na forma:nnn
 |
n
n
n
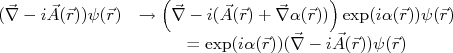 |
n
n
n
 |
n
n
 . Este termo é bastante similar ao potencial vetor encontrado nas Eq. Maxwell para o eletromagnetismo. Esta introdução é interpretada como a necessidade de introduzir novos campos na hamiltoniana do sistema de modo a manter o sistema simétrico por transformações locais. Estes campos são denominados campos de calibre e levam à introdução de forças físicas reais no problema.
. Este termo é bastante similar ao potencial vetor encontrado nas Eq. Maxwell para o eletromagnetismo. Esta introdução é interpretada como a necessidade de introduzir novos campos na hamiltoniana do sistema de modo a manter o sistema simétrico por transformações locais. Estes campos são denominados campos de calibre e levam à introdução de forças físicas reais no problema. n
nEm um problema físico mais complexo, sujeito a transformações locais mais elaboradas, pode ser necessário introduzir vários campos de calibre para preservar a simetria do sistema por estas transformações locais. Isso implica na adição de forças físicas adicionais no sistema para manter estas simetrias. Podemos pensar da maneira invertida: forças físicas são originadas em um sistema de modo a preservar a simetria desses sistemas em transformações locais. Este princípio, conhecido como princípio de calibre (ou, do Inglês, Gauge Principle) é fundamental na construção de teorias físicas para as interações fundamentais.nn
Leitura recomendada
n- n
- Capítulo X do livro “Introducion to Nuclear and Particle Physics”, Ashok Das e Thomas Ferbel.n
- Capítulo 4 do livro “Introduction to Elementary Particles”, David Griffths.n
n
Exercícios
n- n
- Mostre (32)n
- Mostre (53)n
Deixe um comentário