nnVersão para impressãon
nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n
nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
nNós estamos habituados a resolver problemas de mecânica quântica utilizando as funções de onda, integrando-as “na força bruta” e usando operadores diferenciais, como momento, sem muito drama. Porém, uma outra formulação, bastante conveniente, vai ser muito útil no decorrer desta disciplina. Podemos aproveitar o fato de que autoestados de operadores hermitianos são ortogonais e, fazendo uma escolha apropriada de base, podemos reescrever diversos operadores em termos de elementos de matrizes. Por conta disso, ao invés de trabalhar na forma “tradicional” para um aluno recém apresentado à mecânica quântica, podemos utilizar de ferramentas de algebra linear e representações matriciais para explorar fenômenos quânticos. Isto vai ser particularmente interessante para descrever os operadores geradores de transformações de simetria. O conjunto de matrizes que definem as operações de simetria constituem um grupo. A teoria de grupos, um ramo da matemática trata em detalhes de questões de simetria. Apesar de não precisarmos, neste nível, lidar em detalhes com estas ferramentas, conhecer alguns conceitos básicos sobre grupos é interessante, pois o jargão associado a eles é bem presente na área de física de partículas. É comum, por exemplo, ouvir que glúons são geradores do grupo SU(3), por exemplo. Saber o que isso significa é um grande passo no entendimento das propriedades deles.
n
nAntes disso, vamos fazer uma breve introdução sobre representação matricial de operadores. Veja as recomendações de leitura, no final desta aula, para referências detalhadas sobre este assunto. Serei bastante breve, afinal este não é um curso de mecânica quântica. Antes, vamos introduzir alguns conceitos sobre grupos.n
n
nUm grupo consiste em um conjunto de elementos (números, matrizes, etc.) que pode ser finito ou não com uma regra bem definida de combinação entre eles. Normalmente esta regra é chamada de multiplicação, mas não necessariamente ser uma multiplicação no sentido 2×3=6 como aprendemos no ensino fundamental. Um grupo deve satisfazer algumas regras simples:n
- n
- Um grupo deve ser um conjunto fechado, isto é, sendo dois elementos quaisquer do grupo,
 e
e  , a combinação entre eles,
, a combinação entre eles, 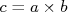 deve ser também um elemento do grupo.n
deve ser também um elemento do grupo.n
- A combinação de elementos deve ser associativa, isto é
 .n
.n
- Deve haver um elemento identidade, isto é
 .n
.n
- Para cada elemento do grupo, deve haver um inverso, de tal forma que
 n
n
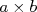 pode ser diferente de
pode ser diferente de  . Grupos onde os elementos são comutativos são chamados de grupos abelianos enquanto grupos cujos elementos não sejam comutativos são chamados de não-abelianos.
. Grupos onde os elementos são comutativos são chamados de grupos abelianos enquanto grupos cujos elementos não sejam comutativos são chamados de não-abelianos.n
nMatrizes constituem grupos. É comum a representação matricial de operadores em mecânica quântica. Assim, será comum a gente se referir a um operador como sendo um elemento de determinado grupo. Estes grupos são identificados por um jargão do tipo U(2), SU(3), O(4), etc. O que significa isso? Para começar, o número entre parênteses indica o tamanho das matrizes do grupo. Por exemplo, o grupo SU(3) consiste em um conjunto de matrizes 3×3. U, SU, O, SO, indicam características dos elementos desse grupo, na forma:n
- n
- U – Os elementos do grupo são unitários. Sendo
 um elemento deste grupo,
um elemento deste grupo, 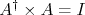 .n
.n
- S – Grupos com a letra S são grupos especiais, isto é, os elementos do grupo possuem determinante unitário. Assim, o grupo SU(3) consiste em um conjunto de matrizes unitárias de 3×3 onde cada matriz possui determinante 1.n
- O – Os elementos do grupo são ortogonais. Sendo
 um elemento deste grupo,
um elemento deste grupo,  , isto é
, isto é  .n
.n
n
nVamos agora discutir como escrevemos operadores e estados como um conjunto de matrizes e vetores. Para isto, vamos utilizar como referência um conjunto de autoestados completos e ortogonais entre si, de modo que
 . Este conjunto pode ser autoestados de uma hamiltoniana, autoestados de momento angular, etc. A escolha de base depende do tipo de problema que se quer estudar. Um estado qualquer,
. Este conjunto pode ser autoestados de uma hamiltoniana, autoestados de momento angular, etc. A escolha de base depende do tipo de problema que se quer estudar. Um estado qualquer,  pode ser decomposta nesta base, através de:n
pode ser decomposta nesta base, através de:nn
n
 (1)n
(1)nn
nAplicar um operador qualquer,
 , neste estado implica em:n
, neste estado implica em:nn
n
 (2)n
(2)nn
nA projeção do estado resultante na j-ésima componente da nossa base é obtida fazendo o produto escalar com o j-ésimo estado desta base, ou seja:n
n
n
 (3)n
(3)nn
nisto é, o operador
 pode ser decomposto em elementos que formam uma matriz representativa deste operador na base
pode ser decomposto em elementos que formam uma matriz representativa deste operador na base  escolhida. Cada elemento de matriz é dado por
escolhida. Cada elemento de matriz é dado por  . Em uma forma matricial:n
. Em uma forma matricial:nn
n
 (4)n
(4)nn
nSimilarmente, podemos escrever que, o produto de dois operadores,
 e
e  pode ser escrito, sabendo que
pode ser escrito, sabendo que  :n
:nn
n
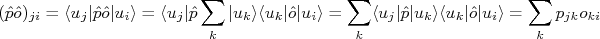 (5)n
(5)nn
nou seja, a multiplicação de dois operadores se transforma em uma simples multiplicação de duas matrizes. O hermitiano conjugado de um operador pode ser calculado facilmente neste notação:n
n
n
 (6)n
(6)nn
nOu seja, o hermitiano conjugado de um operador corresponde à matriz de complexos conjugados transposta do operador original. O produto escalar entre dois estados pode ser escrito na forma:n
n
n
 (7)n
(7)nn
nque, em notação matricial siginifica realizar a multiplicação entre dois vetores na forma:n
n
n
 (8)n
(8)nn
nE, para finalizar, encontrar autovalores de um operador significa resolver a equação

n
n
 (9)nn
(9)nnn
nque tem solução se:n
n
n
 (10)n
(10)nn
nAhhhh, para ninguém falar que eu não mostrei nenhum exemplo prático de um grupo, vou utilizar o exemplo do “Introduction to Nuclear and Particle Physics”, Ashok Das e Thomas Ferbel, apêndice D. Vamos construir um grupo que consiste de todos os números reais, positivos e negativos. Vamos chamar este grupo de
 . Cada elemento do grupo,
. Cada elemento do grupo,  corresponde a um número real
corresponde a um número real  . Vamos definir a multiplicação de dois membros deste grupo como sendo:n
. Vamos definir a multiplicação de dois membros deste grupo como sendo:nn
n
 (11)n
(11)nn
nÉ fácil ver que
 e assim
e assim  , ou seja a operação multiplicativa é associativa. Podemos definir o elemento identidade do grupo como sendo
, ou seja a operação multiplicativa é associativa. Podemos definir o elemento identidade do grupo como sendo  , assim:n
, assim:nn
n
 (12)n
(12)nn
nFinalmente, para um dado elemento do grupo
 , podemos identificar o seu inverso como sendo
, podemos identificar o seu inverso como sendo  , de modo que:n
, de modo que:nn
n
 (13)n
(13)nn
nOu seja, todos os números reais constituem um grupo onde definimos a operação multiplicativa entre dois elementos deste grupo como a soma dos seus valores, respeitando todas as condições para que este conjunto constitua um grupo.n
Leitura recomendada
n- n
- Apêndice D do livro “Introduction to Nuclear and Particle Physics”, Ashok Das e Thomas Ferbel.n
- Capítulo 3 do livro “Introduction to Quantum Mechanics”, David Griffths.n
- Capítulo 2 do livro “Quantum Mechanics”, Cohen-Tannoudji.n
- Capítulo 1 do livro “Modern Quantum Mechanics”, J. J. Sakurai.n
Deixe um comentário