nnVersão para impressãon
nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n
nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
nNormalmente nós somos introduzidos ao momento angular em mecânica quântica a partir da relação  e depois introduzimos o conceito de spin como uma forma de momento angular. Do ponto de vista macroscópico, interpretamos spin como sendo um momento angular intrínseco do objeto como a soma de todos os pequenos momentos angulares
e depois introduzimos o conceito de spin como uma forma de momento angular. Do ponto de vista macroscópico, interpretamos spin como sendo um momento angular intrínseco do objeto como a soma de todos os pequenos momentos angulares 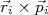 das partículas que constituem este corpo em torno de um eixo de rotação. Até aí tudo bem, podemos viver com esta simplificação. O problema surge quando tentamos adaptar esta definição a partículas elementares e torna-se comum surgirem interpretações de que o spin do elétron, por exemplo, seria uma rotação desta partícula em torno do seu eixo. Isto não é apropriado. Não tem sentido falar em dimensões do elétron e, portanto, não tem sentido falar em movimento de rotação em torno do seu eixo. Neste sentido, não vamos partir da definição
das partículas que constituem este corpo em torno de um eixo de rotação. Até aí tudo bem, podemos viver com esta simplificação. O problema surge quando tentamos adaptar esta definição a partículas elementares e torna-se comum surgirem interpretações de que o spin do elétron, por exemplo, seria uma rotação desta partícula em torno do seu eixo. Isto não é apropriado. Não tem sentido falar em dimensões do elétron e, portanto, não tem sentido falar em movimento de rotação em torno do seu eixo. Neste sentido, não vamos partir da definição  e, conhecendo os operadores momento e posição deduzir os operadores de momento angular e suas regras de comutação. Vamos partir da noção de uma transformação de simetria por rotação de um sistema de coordenadas qualquer (que, por acaso, podem ser, no caso particular, espaciais) e deduzir propriedades dos operadores de rotação.n
e, conhecendo os operadores momento e posição deduzir os operadores de momento angular e suas regras de comutação. Vamos partir da noção de uma transformação de simetria por rotação de um sistema de coordenadas qualquer (que, por acaso, podem ser, no caso particular, espaciais) e deduzir propriedades dos operadores de rotação.n
n
nVamos agora explorar um pouco rotação em um sistema de 3 coordenadas. A rotação em torno de dada um desses eixos (1, 2 ou 3) de um ângulo  pode ser estrita através de três matrizes, uma para cada eixo, de modo que
pode ser estrita através de três matrizes, uma para cada eixo, de modo que  , sendo
, sendo  matrizes dadas por:n
matrizes dadas por:n
n
n
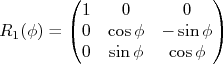 n
n n
n (1)n
(1)nn
nVamos analisar este problema sob o ponto de vista de rotações infinitesimais (nós já vimos que uma transformação contínua de simetria pode ser representada por uma série de transformações infinitesimais). Isso facilita bastante a interpretação pois nos livramos de funções trigonométricas. Expandindo os senos e cossenos em séries de Taylor e, desprezando todos os termos de ordem maior que a de potência 2, fazendo
 , as matrizes em (1) tornam-se:n
, as matrizes em (1) tornam-se:nn
n
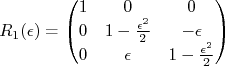 n
n n
n (2)n
(2)nn
nVamos agora tomar um sistema qualquer e fazer uma rotação infinitesimal em torno do eixo-1 e, em seguida, em torno do eixo-2. Isso equivale a fazer uma rotação por uma matriz tal que
 . Podemos fazer o mesmo com sequência invertida, isto é, primeiro uma rotação em torno do eixo-2 e, em seguida, em torno do eixo-1. Isto equivale a fazer uma rotação do tipo
. Podemos fazer o mesmo com sequência invertida, isto é, primeiro uma rotação em torno do eixo-2 e, em seguida, em torno do eixo-1. Isto equivale a fazer uma rotação do tipo  . Estas rotações são idênticas? Isto pode ser verificado através da operação
. Estas rotações são idênticas? Isto pode ser verificado através da operação  . Caso estas rotações sejam idênticas, esta operação resulta em zero. Fazendo esta conta, desprezando todos os termos de ordem maior que a quadrática, temos:n
. Caso estas rotações sejam idênticas, esta operação resulta em zero. Fazendo esta conta, desprezando todos os termos de ordem maior que a quadrática, temos:nn
n
 (3)n
(3)nn
nisto é, as matrizes de rotação não comutam entre si, o que significa que grupos de rotação são não-abelianos. Este é um resultado bastante conhecido em mecânica classica, onde o efeito de subtrair rotações em dois eixos invertidas corresponde a uma rotação no terceiro eixo do sistema.
n
nAgora vamos dar o salto quântico: Vamos definir três operadores
 , responsáveis por rotações em três eixos (aqui mudei o índice de 1,2,3 para x,y,z porque é a notação mais comum em livros didáticos). O operador de rotação infinitesimal para cada um destes geradores pode ser escrito, como vimos:n
, responsáveis por rotações em três eixos (aqui mudei o índice de 1,2,3 para x,y,z porque é a notação mais comum em livros didáticos). O operador de rotação infinitesimal para cada um destes geradores pode ser escrito, como vimos:nn
n
 (4)n
(4)nn
nVamos encontrar relações de comutação para os operadores
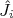 que respeitem as regras de rotações em torno desses três eixos, ou seja,
que respeitem as regras de rotações em torno desses três eixos, ou seja,  . Substituindo (4) nesta expressão temos:n
. Substituindo (4) nesta expressão temos:nn
n

n
n

n
n

n
n

n
n
![[\hat{J}_x,\hat{J}_y] = i\hat{J}_z [\hat{J}_x,\hat{J}_y] = i\hat{J}_z](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/51fc5c968d6f136d9c29079ab7c0ec19.png) (5)n
(5)nn
nA expressão em (5) estabelece a relação de comutação entre os operadores de modo que a transformação de simetria proposta tenha as propriedades de uma rotação em torno de um eixo definido. Pode-se demonstrar estas relações para as outras rotações possíveis, de modo a escrever a relação geral de comutadores entre os operadores geradores de rotação, na forma:n
n
n
![[\hat{J}_i,\hat{J}_j]=i\varepsilon_{ijk}\hat{J}_k [\hat{J}_i,\hat{J}_j]=i\varepsilon_{ijk}\hat{J}_k](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/0ca73d1f491bc0fb0cfdcb04737dde1c.png) (6)n
(6)nn
nQue são as relações de comutação conhecidas para os operadores de momento angular. Note que as relações em (6) podem ser deduzidas facilmente através da definição de momento angular em termos dos operadores de momento linear e posição. Contudo, a dedução que fizemos não necessita da representação de que estes operadores de momento angular estão relacionados a movimentos de rotação em torno de um eixo. Na nossa definição, os operadores de momento angular nada mais são do que geradores de transformações de rotação do sistema em torno de um eixo fixo. E, com base nas relações em (6) vamos ser capazer de explorar diversas características desses operadores.n
n
nA primeira característica é o fato de estes operadores não comutarem entre si. Isto torna impossível encontrar uma base composta por auto-estados simulatâneos destes três operadores. Vamos considerar, agora, um novo operador,
 , em analogia ao módulo de um vetor composto pelas três componentes deste operador momento angular. É fácil mostrar que este operador comuta com qualquer uma das suas componentes:n
, em analogia ao módulo de um vetor composto pelas três componentes deste operador momento angular. É fácil mostrar que este operador comuta com qualquer uma das suas componentes:nn
n
![[\hat{J}^2,\hat{J}_z] = [\hat{J}_x\hat{J}_x + \hat{J}_y\hat{J}_y + \hat{J}_z\hat{J}_z,\hat{J}_z] = [\hat{J}_x\hat{J}_x + \hat{J}_y\hat{J}_y ,\hat{J}_z] [\hat{J}^2,\hat{J}_z] = [\hat{J}_x\hat{J}_x + \hat{J}_y\hat{J}_y + \hat{J}_z\hat{J}_z,\hat{J}_z] = [\hat{J}_x\hat{J}_x + \hat{J}_y\hat{J}_y ,\hat{J}_z]](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/207984fb1340a26e8a7d2bcc654d47b3.png)
n
n
![[\hat{J}^2,\hat{J}_z] = [\hat{J}_x\hat{J}_x ,\hat{J}_z] + [\hat{J}_y\hat{J}_y ,\hat{J}_z] [\hat{J}^2,\hat{J}_z] = [\hat{J}_x\hat{J}_x ,\hat{J}_z] + [\hat{J}_y\hat{J}_y ,\hat{J}_z]](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/15b97e896380f8a357902022f61d984b.png)
n
n
![[\hat{J}^2,\hat{J}_z] =\hat{J}_x[\hat{J}_x ,\hat{J}_z] + [\hat{J}_x ,\hat{J}_z]\hat{J}_x + \hat{J}_y[\hat{J}_y ,\hat{J}_z] + [\hat{J}_y ,\hat{J}_z]\hat{J}_y [\hat{J}^2,\hat{J}_z] =\hat{J}_x[\hat{J}_x ,\hat{J}_z] + [\hat{J}_x ,\hat{J}_z]\hat{J}_x + \hat{J}_y[\hat{J}_y ,\hat{J}_z] + [\hat{J}_y ,\hat{J}_z]\hat{J}_y](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/f3d78feb7a012fbf57bf6b2e402aa12c.png)
n
n
![[\hat{J}^2,\hat{J}_z] =\hat{J}_x(-i\hat{J}_y) + (-i\hat{J}_y)\hat{J}_x + \hat{J}_y(i\hat{J}_x) + (i\hat{J}_x)\hat{J}_y [\hat{J}^2,\hat{J}_z] =\hat{J}_x(-i\hat{J}_y) + (-i\hat{J}_y)\hat{J}_x + \hat{J}_y(i\hat{J}_x) + (i\hat{J}_x)\hat{J}_y](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/746a7ed0397fa7666cd196c5762cc3fa.png)
n
n
![[\hat{J}^2,\hat{J}_z] = 0 [\hat{J}^2,\hat{J}_z] = 0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/e29b59e380da9e668f6bfe6621070995.png) (7)n
(7)nn
nO mesmo pode ser mostrado para as outras componentes. Isto significa que podemos construir uma base ortogonal composta por auto-estados simulatâneos de
 e uma de suas componentes. Por convenção, é comum escolher esta componente como sendo
e uma de suas componentes. Por convenção, é comum escolher esta componente como sendo  . Estes estados são representados pelo vetor
. Estes estados são representados pelo vetor 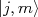 , onde:n
, onde:nn
n
 (8)n
(8)nn
ncom
 um número inteiro ou semi-inteiro e
um número inteiro ou semi-inteiro e  , variando de uma unidade entre esses limites. Nós não vamos demonstrar isto aqui. Uma boa demonstração pode ser obtida na seção 3.5 do livro “Modern Quantum Mechanics”, J. J. Sakurai. Em linhas gerais a obtenção desses autoestados parte da criação de operadores escada
, variando de uma unidade entre esses limites. Nós não vamos demonstrar isto aqui. Uma boa demonstração pode ser obtida na seção 3.5 do livro “Modern Quantum Mechanics”, J. J. Sakurai. Em linhas gerais a obtenção desses autoestados parte da criação de operadores escada  , que satisfazem (também demonstrado neste capítulo do Sakurai):
, que satisfazem (também demonstrado neste capítulo do Sakurai):n
n
n
 (9)n
(9)nnEstes operadores escadas são extremamente úteis para encontrar a forma matricial de operadores de momento angular, já que:n
n
n
 (10)n
(10)nn
nnEm muitas situações torna-se necessário realizar adições de momento angular. Por exemplo, em um sistema de duas partículas, cada uma de estados de momento angular
 e
e  , resulta em um sistema cujo momento angular total
, resulta em um sistema cujo momento angular total  . Em muitos casos a descrição do sistema na base
. Em muitos casos a descrição do sistema na base  e sim na base
e sim na base  . Neste caso, um estado em uma base pode ser obtido a partir dos estados em outra base através de:n
. Neste caso, um estado em uma base pode ser obtido a partir dos estados em outra base através de:nn
n
 n
nn
n
 são denominados coeficientes de Clebsh-Gordan e podem ser obtidos de tabelas ou calculados manualmente. Uma propriedade importante destes coeficientes é que eles se anulam se
são denominados coeficientes de Clebsh-Gordan e podem ser obtidos de tabelas ou calculados manualmente. Uma propriedade importante destes coeficientes é que eles se anulam se  , o que reduz consideravelmente o número de combinações possíveis.nnn
, o que reduz consideravelmente o número de combinações possíveis.nnn
Sistemas de dois níveis: spin, isospin, … = 1/2
nTalvez o mais importante estado de momento angular é aquele com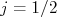 . O próton, neutron, todos os quarks, léptons, possui esta propriedade intrínseca, que chamamos de spin. Quando fomos discutir equação de Dirac, o spin surgirá naturalmente como propriedade dessas partículas. Por enquanto vamos apenas discutir um pouco algumas propriedades destes sistemas. Inicialmente vamos construir os operadores para
. O próton, neutron, todos os quarks, léptons, possui esta propriedade intrínseca, que chamamos de spin. Quando fomos discutir equação de Dirac, o spin surgirá naturalmente como propriedade dessas partículas. Por enquanto vamos apenas discutir um pouco algumas propriedades destes sistemas. Inicialmente vamos construir os operadores para 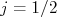 , que, para adotar uma convenção mais familiar, chamaremos de
, que, para adotar uma convenção mais familiar, chamaremos de  . Utilizando uma base composta de auto-estados de
. Utilizando uma base composta de auto-estados de  e
e  , que tem apenas dois vetores, na forma:n
, que tem apenas dois vetores, na forma:nn
n
 (11)n
(11)nn
nUtilizando as relações em (8) é fácil escrever que:n
n
n
 (12)n
(12)nn
nOs operadores
 e
e 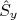 podem ser obtidos através dos operadores
podem ser obtidos através dos operadores  e
e 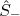 . Utilizando (10), o operador
. Utilizando (10), o operador  tem todos os elementos nulos, exceto o elemento
tem todos os elementos nulos, exceto o elemento 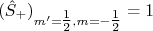 . No caso do
. No caso do 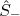 , todos elementos são nulos exceto
, todos elementos são nulos exceto 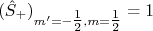 . Da definição destes operadoes escada, podemos escrever que
. Da definição destes operadoes escada, podemos escrever que  e
e  , escrevemos:n
, escrevemos:nn
n
 (13)n
(13)nn
nEm geral, costuma-se utilizar a notação
 onde
onde  são denominadas de matrizes de Pauli cujas matrizes
são denominadas de matrizes de Pauli cujas matrizes  constituem os elementos do grupo SU(2). As matrizes do grupo SU(2) são tais que:n
constituem os elementos do grupo SU(2). As matrizes do grupo SU(2) são tais que:nn
n
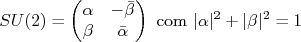 (14)n
(14)nn
nO estado mais geral de uma partícula de spin 1/2 pode ser escrito como sendo:
n
n
 (15)n
(15)nn
nOu seja,
 fornece a probabilidade de a partícula ser encontrada com spin com projeção em z +1/2. O mesmo vale para
fornece a probabilidade de a partícula ser encontrada com spin com projeção em z +1/2. O mesmo vale para  . Note que, neste caso,
. Note que, neste caso,  para manter o estano normalizado. É comum chamar estes sistemas de dois níveis de espinores (spinnors), ou objetos de duas componentes, algo intermediário entre objetos escalares (uma componentes) e vetoriais (três componentes). nn
para manter o estano normalizado. É comum chamar estes sistemas de dois níveis de espinores (spinnors), ou objetos de duas componentes, algo intermediário entre objetos escalares (uma componentes) e vetoriais (três componentes). nn
Leitura recomendada
n- n
- Capítulo 3 do livro “Modern Quantum Mechanics”, J. J. Sakurai.n
- Capítulo 4 do livro “Introduction to Elementary Particles”, David Griffths.n
n
Exercícios
n- n
- Obtenha os operadores
 ,
,  ,
,  e
e  , na forma matricial, para
, na forma matricial, para  .n
.n
- Mostre que o operador
 é responsável por uma rotação em torno deste eixo por um ângulo
é responsável por uma rotação em torno deste eixo por um ângulo  qualquer. Dica: Uma rotação qualquer de um ângulo
qualquer. Dica: Uma rotação qualquer de um ângulo  em torno de um eixo
em torno de um eixo 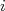 é dada por
é dada por  . Calcule o valor esperado para
. Calcule o valor esperado para  e
e  após esta rotação. Dica 2: Utilize para isso o teorema de Baker-Hausdorff.n
após esta rotação. Dica 2: Utilize para isso o teorema de Baker-Hausdorff.n
- Um estado composto de quarks+antiquarks u e d, cada um com isospin 1/2, pode formar dois sistemas de isospin total, 0 e 1. Um destes estados é singleto, o de isospin 0 e o outro, de isospin 1, tripleto. Tomando a notação de que
 corresponde a um quark com
corresponde a um quark com  e
e  corresponde a um quark com
corresponde a um quark com 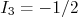 , podemos escrever quatro estados compostos por duas partículas de isospin 1/2, que são:
, podemos escrever quatro estados compostos por duas partículas de isospin 1/2, que são:
n
n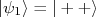
n
n
n
n
n
n
n
nUtilizando argumentos de simetria de rotação, mostre que 3 destes estados estão relacionados por rotações de isospin em torno do eixo 2, que correspondem ao estado de isospin total 1 e que um destes estados é invariante por qualquer tipo de rotação, correspondente ao estado de isospin total 0. Identifique, olhando no Particle Data Group, quais mésons correspondem a cada um destes estados.n- ]]>
Deixe um comentário