nnVersão para impressãon
nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n
nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
nHá algumas simetrias em física de partículas que não são contínuas como as que estudamos anteriormente. Vamos discutir um pouco estas simetrias aqui. São elas: paridade (P), inversão de carga (C) e inversão temporal (T). Elas, individualmente, são violadas em algum momento das interações entre partículas fundamentais. Contudo, as três juntas, constituem uma importante invariância na física de partículas elementares, a invariância CPT. O Teorema CPT, primeiramente demonstrado por Pauli, Lüders e Bell atesta que qualquer teoria que seja invariante por transformações de Lorentz deve ser invariante pelo conjunto de transformações de paridade, conjunção de carga e inversão temporal. A prova deste teorema envolve teoria quântica de campos e está bastante além do escopo desta disciplina. Em todo caso, um trabalho recente provando CPT pode ser encontrado neste link. O teorema CPT tem consequências importantes na física de partículas elementares tais como:
n
nn
- n
- Partículas de spin inteiro satisfazem a estatística de Bose-Einstein enquanto partículas de spin semi-inteiro, a estatística de Fermi-Dirac.n
- Partículas e antipartículas devem ter a mesma massa e vida média, enquanto os números quânticos internos de antipartículas são opostos aos de partículas.n
nnDe fato, CPT tem sido testado experimentalmente com elevado grau de precisão. Um review destes testes pode ser encontrado do Particle Data Group, neste link. Por exemplo, na figura 1 mostramos a diferença entre massa e vida média de káons neutros, condizente com zero com precisão de 10-18 GeV. (lembre-se que a massa do káon é da ordem de 400 MeV!).n
n
n

nFigura 1 – Intervalos de confiança para diferença de massa e vida média para káons neutros e sua antipartícula (Fonte: PDG).
n
nnEstas três simetrias correspondem a um grupo bastante simples, composto de dois elementos apenas, um deles é o elemento identidade e o outro tal que
 . Estas transformações são representadas por operadores unitários,
. Estas transformações são representadas por operadores unitários,  (ou anti-unitários, no caso da inversão temporal). Se estas transformações forem simetrias do sistema físico, então, como vimos,
(ou anti-unitários, no caso da inversão temporal). Se estas transformações forem simetrias do sistema físico, então, como vimos, ![[U,H]=0 [U,H]=0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/3fd9776555103e0499bb75c50ba6a717.png) e, pelas características deste grupo:n
e, pelas características deste grupo:nn
n
 (1)
(1)n
no que faz com que os autovalores destes operadores sejam
 . Vamos olhar um pouco em detalhes cada uma destas transformações.
nnn
. Vamos olhar um pouco em detalhes cada uma destas transformações.
nnn
Paridade
nO operador paridade pode ser definido como o operador que espelha as coordenadas espaciais de um sistema quântico, ou seja:nn (2)
(2)n
nnnOu ainda:
n
n
 (3)
(3)n
nnnAplicando novamente o operador paridade em (2), temos:nn
 (4)
(4)nnOu seja, o operador
 é unitário. Isso sugere que os auto-estados do operador paridade possuam auto-valores
é unitário. Isso sugere que os auto-estados do operador paridade possuam auto-valores  , ou seja:nn
, ou seja:nn
 (5)
(5)nnAs únicas funções cujo espelhamento das coordenadas espaciais retornam a mesma função, mudando (ou não) apenas os seus sinais são as chamadas funções pares e ímpares. Em uma função par
 enquanto em uma função ímpar,
enquanto em uma função ímpar,  .n
nUma consequência óbvia é que a qualquer auto-estado que seja uma função par ou ímpar por reflexão das suas coordenadas também será um auto-estado da paridade. Assim, caso os auto-estados de uma Hamiltoniana sejam funções pares ou ímpares, a paridade será uma constante do sistema. Para que os auto-estados de uma Hamiltoniana possuam paridade bem definidas é necessário que o potencial de interação seja uma função par. Isso pode ser demonstrado calculando-se explicitamente o comutador
.n
nUma consequência óbvia é que a qualquer auto-estado que seja uma função par ou ímpar por reflexão das suas coordenadas também será um auto-estado da paridade. Assim, caso os auto-estados de uma Hamiltoniana sejam funções pares ou ímpares, a paridade será uma constante do sistema. Para que os auto-estados de uma Hamiltoniana possuam paridade bem definidas é necessário que o potencial de interação seja uma função par. Isso pode ser demonstrado calculando-se explicitamente o comutador ![[H,P] [H,P]](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/47a3bfc5c81da0c806ef51bc677e9639.png) . Esse será nulo se o potencial de interação for par. n
nEm um sistema cujo potencial é radial, pode-se escrever a função de onda como sendo:nn
. Esse será nulo se o potencial de interação for par. n
nEm um sistema cujo potencial é radial, pode-se escrever a função de onda como sendo:nn
 (6)
(6)nnAplicando o operador paridade nessa função de onda, temos:nn
 (7)
(7)nnIsto é, a paridade de uma função de onda obtida de um potencial central é definida pelo momento angular e será par se
 for par e ímpar, se
for par e ímpar, se  for ímpar. Em um sistema de múltiplas partículas, o estado final desse sistema pode ser escrito como o produto dos estados individuais de cada uma das partículas. Se todas as partículas possuírem paridade bem definida, a paridade do sistema final será o produto das paridades individuais.n
nEm sistemas quânticos, além da paridade devida às propriedades espaciais das funções de onda, as partículas ainda podem apresentar uma paridade intrínseca que é independente das coordenadas espaciais, como em (7). Assim, é comum definir a paridade total de um estado quântico como sendo:n
for ímpar. Em um sistema de múltiplas partículas, o estado final desse sistema pode ser escrito como o produto dos estados individuais de cada uma das partículas. Se todas as partículas possuírem paridade bem definida, a paridade do sistema final será o produto das paridades individuais.n
nEm sistemas quânticos, além da paridade devida às propriedades espaciais das funções de onda, as partículas ainda podem apresentar uma paridade intrínseca que é independente das coordenadas espaciais, como em (7). Assim, é comum definir a paridade total de um estado quântico como sendo:nn
n
 (8)
(8)n
nO estudo detalhado de partículas mostra que bósons possuem a mesma paridade que suas antipartículas enquanto férmions possuem paridade invertida em relação as suas antipartículas. Em uma reação (ou decaimento) do tipo
 , por exemplo, caso haja conservação de partidade tem-se que
, por exemplo, caso haja conservação de partidade tem-se que  onde
onde  corresponde ao momento angular relativo entre as partículas finais.
corresponde ao momento angular relativo entre as partículas finais.n
nTomemos como exemplo, o decaimento forte
 , onde
, onde  é um nucleon. Conservando a paridade, temos
é um nucleon. Conservando a paridade, temos  . Sendo a paridade do píon -1 e a paridade de um nucleon positiva (por convenção, define-se a paridade do próton, nêutron e
. Sendo a paridade do píon -1 e a paridade de um nucleon positiva (por convenção, define-se a paridade do próton, nêutron e  como sendo +1), leva-nos a concluir que
como sendo +1), leva-nos a concluir que  . A análise do decaimento desta partícula, no seu referencial de repouso, mostra que
. A análise do decaimento desta partícula, no seu referencial de repouso, mostra que  , o que nos leva a concluir que a paridade desta partícula é
, o que nos leva a concluir que a paridade desta partícula é  .nn
.nnn
nA conservação da paridade começou a ser questionada nos anos 50, com os estudos das partículas entranhas. Naquela época conheciam-se duas partículas estranhas, o
 e
e  (que mais tarde foram chamadas de kaons) que decaiam, respectivamente, em
(que mais tarde foram chamadas de kaons) que decaiam, respectivamente, em  e
e  . Como todas estas partículas têm spin 0, o momento angular relativo entre as partículas no estado final deve ser
. Como todas estas partículas têm spin 0, o momento angular relativo entre as partículas no estado final deve ser  . Acontece que, a paridade intrínseca de píons é negativa. Assim, a conservação de paridade nos levaria a concluir que o estado
. Acontece que, a paridade intrínseca de píons é negativa. Assim, a conservação de paridade nos levaria a concluir que o estado  teria paridade positiva enquanto o estado
teria paridade positiva enquanto o estado  teria paridade negativa. Acontece que estas partículas possuem exatamente a mesma massa e mesma vida média, o que sugeria que elas seriam a mesma partícula. Como conciliar estes fatos? T. D. Lee e C. N. Yang perceberam que não havia nenhuma justificativa para que a paridade fosse conservada em interações fracas e eles postularam que estas duas partículas, na verdade, era uma só, o
teria paridade negativa. Acontece que estas partículas possuem exatamente a mesma massa e mesma vida média, o que sugeria que elas seriam a mesma partícula. Como conciliar estes fatos? T. D. Lee e C. N. Yang perceberam que não havia nenhuma justificativa para que a paridade fosse conservada em interações fracas e eles postularam que estas duas partículas, na verdade, era uma só, o  e que os dois decaimentos seriam possíveis por conta da não conservação de paridade nestas interações. A não conservação de paridade em interações fracas foi confirmada experimentalmente por Madame Wu e colaboradores, no clássico experimento de decaimento beta do cobalto-60, esquematizado na figura 2.
e que os dois decaimentos seriam possíveis por conta da não conservação de paridade nestas interações. A não conservação de paridade em interações fracas foi confirmada experimentalmente por Madame Wu e colaboradores, no clássico experimento de decaimento beta do cobalto-60, esquematizado na figura 2.n
n

nFigura 2 – Violação de paridade em decaimentos beta.
Inversão temporal
nA inversão temporal altera o fluxo de tempo em um sistema. Esta transformação é realizada de modo que:nn
n
 (9)
(9)n
n
 (10)
(10) não mantém (10) invariante por inversão temporal. Contudo, uma transformação do tipo
não mantém (10) invariante por inversão temporal. Contudo, uma transformação do tipo  mantém a invariância de (10). É por conta desta necessidade de se tomar o complexo conjugado na transformação que o operador inversão temporal não é unitário e não é possível definir números quânticos para o operador
mantém a invariância de (10). É por conta desta necessidade de se tomar o complexo conjugado na transformação que o operador inversão temporal não é unitário e não é possível definir números quânticos para o operador  . Contudo, uma consequência direta de simetria por inversão temporal se faz presente na medida de elementos de matriz para transições entre estados quânticos distintos. Em um sistema simétrico por inversão temporal, os módulos dos elementos de matriz para um processo qualquer, devem ser iguais, ou seja:n
. Contudo, uma consequência direta de simetria por inversão temporal se faz presente na medida de elementos de matriz para transições entre estados quânticos distintos. Em um sistema simétrico por inversão temporal, os módulos dos elementos de matriz para um processo qualquer, devem ser iguais, ou seja:nn
n
 (11)
(11) e
e  mostrando taxas de transição significativamente diferentes entre eles.nn
mostrando taxas de transição significativamente diferentes entre eles.nn
Inversão de carga
nNa operação de inversão de carga, espaço e tempo não são alterados. Esta operação altera somente propriedades internas do estado quântico. A operação de inversão de carga atua trocando o sinal da carga elétrica, ou seja:nn
n
 (12)
(12) , similar à paridade. Em um estado quântico, o efeito prático do operação de inversão de carga é transformar um estado de partícula para antipartícula, e vice-versa, de forma que:n
, similar à paridade. Em um estado quântico, o efeito prático do operação de inversão de carga é transformar um estado de partícula para antipartícula, e vice-versa, de forma que:nn
n
 (13)
(13) . Isto é relativamente fácil de ser compreendido. As Equações de Maxwell são invariantes por troca de carga elétrica. Porém, a inversão de carga transforma os campos elétricos e magnéticos na forma:n
. Isto é relativamente fácil de ser compreendido. As Equações de Maxwell são invariantes por troca de carga elétrica. Porém, a inversão de carga transforma os campos elétricos e magnéticos na forma:nn
n
 e
e  (14)
(14) .n
.nn
nAssim, como a paridade, se a inversão de carga corresponder a uma simetria do sistema quântico, sua paridade deve ser conservada. Por exemplo, como as eq. de Maxwell são invariantes por inversão de carga, transições eletromagnéticas devem conservar esta quantidade. Sendo assim, é fácil deduzir, a partir do decaimento do píon neutro
 que
que  . Isto indica também a impossibilidade de um píon neutro decair em três fótons, pois, neste caso, não haveria conservação de paridade de carga em transições eletromagnéticas. Por outro lado, interações fracas não necessariamente conservam a paridade de carga. Um exemplo típico é o neutrino, que veremos mais adiante.n
nn
. Isto indica também a impossibilidade de um píon neutro decair em três fótons, pois, neste caso, não haveria conservação de paridade de carga em transições eletromagnéticas. Por outro lado, interações fracas não necessariamente conservam a paridade de carga. Um exemplo típico é o neutrino, que veremos mais adiante.n
nn
O káon – CP e flutuação de estranheza
nEm um tempo distante, onde káons não eram chamados de káons e sim por nomes estranhos, como theta e táu, estudava-se o decaimento dessas partículas. Nós já discutimos um pouco o decaimento do e
e  em dois e três píons e as consequências disso na conservação de paridade. O análogo pode ser explorado para as versões neutras dessas partículas, o
em dois e três píons e as consequências disso na conservação de paridade. O análogo pode ser explorado para as versões neutras dessas partículas, o 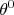 e
e  , que podem decair em dois (no caso do
, que podem decair em dois (no caso do  ) e três (no caso do
) e três (no caso do  ) píons. Vamos tentar estudar em um pouco mais de detalhes a relação entre estes estados e os káons, como os entendemos hoje. Káons podem ser produzidos em colisões fortes de várias maneiras. Em geral um feixe de píons ou káons carregados incide sobre alvos contendo prótons e nêutrons. Algumas reações podem ocorrer produzindo káons neutros. Por exemplo, na figura 3 vê-se a reação
) píons. Vamos tentar estudar em um pouco mais de detalhes a relação entre estes estados e os káons, como os entendemos hoje. Káons podem ser produzidos em colisões fortes de várias maneiras. Em geral um feixe de píons ou káons carregados incide sobre alvos contendo prótons e nêutrons. Algumas reações podem ocorrer produzindo káons neutros. Por exemplo, na figura 3 vê-se a reação  realizada no Bevatron, no laboratório de Berkeley, onde os traços das partículas carregadas são identificados por uma câmara de bolhas em baixa temperatura. Na figura 4 tem-se o esquema desta reação identificando as partículas. Tanto o káon neutro quanto o lambda não deixam registro na figura mas, após percorrerem um certo caminho, decaem em partículas carregadas, de cargas opostas. Este decaimento é conhecido como V0 por lembrar a letra V e o zero, por indicar a carga da partícula mãe.
realizada no Bevatron, no laboratório de Berkeley, onde os traços das partículas carregadas são identificados por uma câmara de bolhas em baixa temperatura. Na figura 4 tem-se o esquema desta reação identificando as partículas. Tanto o káon neutro quanto o lambda não deixam registro na figura mas, após percorrerem um certo caminho, decaem em partículas carregadas, de cargas opostas. Este decaimento é conhecido como V0 por lembrar a letra V e o zero, por indicar a carga da partícula mãe.n
n

nFigura 3 – reação de produção de káon neutro e lambda a partir de uma colisão entre píon carregado e próton no Bevatron, em Berkeley.
n
n

nFigura 4 – Esquema da reação mostrada na figura 3, identificando as partículas.
n
n
 onde
onde  é o comprimento de decaimento e
é o comprimento de decaimento e  é o tempo no referencial do káon. Medidas de tempo de decaimento de káons neutros (e seus antikáons) mostram a presença de modos de decaimento com duas vidas-média distintas, uma da ordem de 10-10 s e outra da ordem de 10-8 s. Hoje em dia conhece-se estes modos de decaimento como káon-short e káon-long, com vidas médias de
é o tempo no referencial do káon. Medidas de tempo de decaimento de káons neutros (e seus antikáons) mostram a presença de modos de decaimento com duas vidas-média distintas, uma da ordem de 10-10 s e outra da ordem de 10-8 s. Hoje em dia conhece-se estes modos de decaimento como káon-short e káon-long, com vidas médias de  e
e  . O interessante disso é que, apesar de káons serem produzidos, em colisões como as mostradas anteriormente, por interações fortes em autoestados bem distintos de estranheza e isospin (calcule S e I da reação acima), diferenciando partícula de antipartícula, eles decaem por interação fraca, permitindo, inclusive o decaimento idêntico para partícula e antipartícula. Por exemplo, káons neutros e suas antipartículas podem decair em estados de dois píons neutros. Estes decaimentos não conservam estranheza, característico das interações fracas. Com base nestes argumentos, podemos inferir que káons e antikáons neutros são autoestados de uma hamiltoniana de interação forte mas não são autoestados da hamiltoniana de interação fraca, que faz com que cada um deles possa decair com duas vidas-média distintas. Vamos então tentar descrever o que acontece com estas partículas.n
. O interessante disso é que, apesar de káons serem produzidos, em colisões como as mostradas anteriormente, por interações fortes em autoestados bem distintos de estranheza e isospin (calcule S e I da reação acima), diferenciando partícula de antipartícula, eles decaem por interação fraca, permitindo, inclusive o decaimento idêntico para partícula e antipartícula. Por exemplo, káons neutros e suas antipartículas podem decair em estados de dois píons neutros. Estes decaimentos não conservam estranheza, característico das interações fracas. Com base nestes argumentos, podemos inferir que káons e antikáons neutros são autoestados de uma hamiltoniana de interação forte mas não são autoestados da hamiltoniana de interação fraca, que faz com que cada um deles possa decair com duas vidas-média distintas. Vamos então tentar descrever o que acontece com estas partículas.nn
nDo ponto de vista da hamiltoniana de interação forte
 (s de strong) káons neutros e antikáons neutros são autoestados desta hamiltoniana. Assim, temos as relações (vou economizar o superescrito de carga para evitar carregar demais na notação. Assim
(s de strong) káons neutros e antikáons neutros são autoestados desta hamiltoniana. Assim, temos as relações (vou economizar o superescrito de carga para evitar carregar demais na notação. Assim  ):n
):nn
n
 (15)
(15) (w de weak) de modo que:n
(w de weak) de modo que:nn
n
 (16)
(16)n
n
 (17)
(17)n
n
 (18)
(18)n
n
 (19)
(19) , de modo que:nn
, de modo que:nnn
n
 (20)
(20)n
n
 (21)
(21) e
e  e os estados em (18) e (19) serem normalizados, é fácil demonstrar que:nn
e os estados em (18) e (19) serem normalizados, é fácil demonstrar que:nnn
n
 (22)
(22)n
n
 (23)
(23)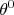 e
e  , que têm vida média curta e longa. Da mesma forma, podemos inverter (22) e (23) e escrever que:n
, que têm vida média curta e longa. Da mesma forma, podemos inverter (22) e (23) e escrever que:nn
n
 (24)
(24)n
n
 (25)
(25)n
nComo estamos examinando os decaimentos desses estados após eles serem produzidos, é importante avaliar a evolução temporal dos mesmos. Após eles serem produzidos por interação forte, o decaimento dos mesmos se dá através de transições por conta de uma hamiltoniana de interação fraca. Construir a hamiltoniana de interação fraca não é nosso objetivo neste momento então vamos construir um modelo efetivo que possa ser parametrizado e aplicado a dados experimentais, com o objetivo de se extrair alguma informação possível de ser interpretada fisicamente. Vamos então representar esta interação por uma hamiltoniana efetiva
 , de tal forma que:n
, de tal forma que:nn
n
 (26)
(26)n
n
 (27)
(27) e
e  matrizes hermitianas. Por conta disso,
matrizes hermitianas. Por conta disso,  não é hermitiana e isso é importante para representar o decaimento do estado. A variação da amplitude do estado
não é hermitiana e isso é importante para representar o decaimento do estado. A variação da amplitude do estado  pode ser calculada como:n
pode ser calculada como:nn
n
 (28)
(28)n
n

n
n

n
n
 (29)
(29) não pode ser hermitiana e que o termo
não pode ser hermitiana e que o termo  da hamiltoniana efetiva corresponde à parte real da energia do estado quântico e, no centro de momento desse estado, deve retornar a massa do mesmo. n
da hamiltoniana efetiva corresponde à parte real da energia do estado quântico e, no centro de momento desse estado, deve retornar a massa do mesmo. nn
nUtilizando como base os estados de partícula e antipartícula para o káon, podemos escrever que, em uma representação de um sistema de dois níveis:n
n
n
 (30)
(30)n
n
 (31)
(31)n
n
 (32)
(32)n
n
 (33)
(33) . De modo a manter a invariância desta hamiltoniana por CPT, ela deve satisfazer a condição
. De modo a manter a invariância desta hamiltoniana por CPT, ela deve satisfazer a condição  , o que torna:n
, o que torna:nn
n
 (34)
(34) e
e  , por outro lado, são autoestados desta hamiltoniana. Lembrando o formato dela em (27), podemos escrever que:n
, por outro lado, são autoestados desta hamiltoniana. Lembrando o formato dela em (27), podemos escrever que:nn
n
 (35)
n
(35)
n (36)
(36)n
n
 (37)
n
(37)
n (38)
n
(38)
n com os tempos de decaimento destes káons através de
com os tempos de decaimento destes káons através de  .
.n
nPodemos escrever (37) e (38) em termos da base definida em (30), usando uma notação similar à mostrada em (31). Deste modo:n
n
n
 (39)
n
(39)
n (40)
(40)
 . Escolhendo
. Escolhendo  e
e  , os estados de káon e antikáons podem ser escritos como: n
, os estados de káon e antikáons podem ser escritos como: nn
n
 (41)
n
(41)
n (42)
(42)
 e
e  obtemos (24) e (25).
obtemos (24) e (25). n
nVamos voltar ao nosso problema inicial, uma colisão como a que acontece na figura 4, onde, no instante inicial, todas as partículas produzidas são káons neutrons. Não há antikáons. A evolução temporal do estado de káons pode ser obtida substituindo (37) e (38) em (41) e, com alguma manipulação algébrica, chega-se à:n
n
n
![|K(t)\rangle = \frac{1}{2p}\left[ p\left( e^{-i(m_s-\frac{i}{2}\gamma_s)t} + e^{-i(m_L-\frac{i}{2}\gamma_L)t} \right ) |K\rangle + q \left( e^{-i(m_s-\frac{i}{2}\gamma_s)t} - e^{-i(m_L-\frac{i}{2}\gamma_L)t} \right ) |\bar K\rangle \right] |K(t)\rangle = \frac{1}{2p}\left[ p\left( e^{-i(m_s-\frac{i}{2}\gamma_s)t} + e^{-i(m_L-\frac{i}{2}\gamma_L)t} \right ) |K\rangle + q \left( e^{-i(m_s-\frac{i}{2}\gamma_s)t} - e^{-i(m_L-\frac{i}{2}\gamma_L)t} \right ) |\bar K\rangle \right]](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/9f7f39fe59247db5fce9c6df6ef29b22.png) (43)
(43)
 ou
ou  que pode ser facilmente calculada a partir de (43), obtendo:n
que pode ser facilmente calculada a partir de (43), obtendo:nn
n
 (44)
n
(44)
n (45)
(45)
 . n
. nn
nNote que há um termo oscilatório nas expressões acima que é presente apenas se houver diferença entre as massas desses káons. Entre 1990 e 1996, no CERN, o exeprimento CPLEAR (figura 5) estudou em detalhes a produção e decaimento de káons, de modo a investigar, não apenas a assimetria em massa
 mas também a violação de CP em interações fracas (mais adiante). O experimento consiste em feixes de antiprótons sobre alvo de próton onde é possível ocorrer as reações
mas também a violação de CP em interações fracas (mais adiante). O experimento consiste em feixes de antiprótons sobre alvo de próton onde é possível ocorrer as reações  e
e  . A seleção de káons neutros ou sua antipartícula é feixa identificando o káon carregado e o píon carregado, como mostra um evento na figura 6.n
. A seleção de káons neutros ou sua antipartícula é feixa identificando o káon carregado e o píon carregado, como mostra um evento na figura 6.nn
n

nFigura 5 – Foto do experimento CPLEAR no CERN.
n
n

nFigura 6 – Um evento típico do experimento CPLEAR no CERN.
n
n
n
n
 (46)
(46)
n
n
 (47)
(47)
n
n

nFigura 7 – Medida de assimetria de massa para káons do experimento CPLEAR.
n
n
n
n
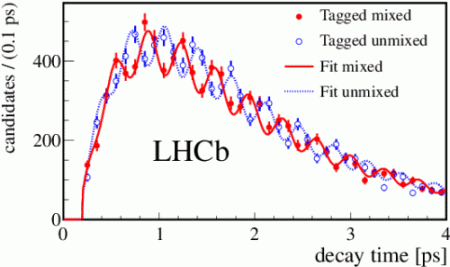
nFigura 8 – Oscilações de mésons B no experimento LHCb, do LHC, no CERN, obtidas recentemente.
n
nNo desenvolvimento que fizemos, se tomarmos
 e
e  , estamos representando estados como os descritos em (22) à (25). Nestes estados, CP é conservada totalmente. Por outro lado, são observados decaimentos do tipo
, estamos representando estados como os descritos em (22) à (25). Nestes estados, CP é conservada totalmente. Por outro lado, são observados decaimentos do tipo  e decaimentos do tipo
e decaimentos do tipo  . O primeiro, com dois píons, tem elevada probabilidade de ocorrer, o que é esperado, por conservar CP. O segundo, em três píons, não conserva CP e ocorre com baixíssima probabilidade (menor que 10-7). Este efeito ocorre também para káons longos, mas invertido, pois a CP para estes káons é invertido em relação aos káons curtos. Este efeito foi observado em 1964 por Fitch e Cronin, que ganharam prêmio Nobel anos mais tarde. O que se conclui disso é que interações fracas violam CP. A conclusão disso é que os autoestados da hamiltoniana fraca não são autoestados simultâneos de CP, isto é,
. O primeiro, com dois píons, tem elevada probabilidade de ocorrer, o que é esperado, por conservar CP. O segundo, em três píons, não conserva CP e ocorre com baixíssima probabilidade (menor que 10-7). Este efeito ocorre também para káons longos, mas invertido, pois a CP para estes káons é invertido em relação aos káons curtos. Este efeito foi observado em 1964 por Fitch e Cronin, que ganharam prêmio Nobel anos mais tarde. O que se conclui disso é que interações fracas violam CP. A conclusão disso é que os autoestados da hamiltoniana fraca não são autoestados simultâneos de CP, isto é,  e
e  , autoestados da hamiltoniana fraca, não seriam autoestados de CP. Contudo, podemos argumentar que, como esta quebra de simetria é pequena, a diferença entre autoestados da hamiltoniana fraca e autoestados de CP deva ser muito pequena, podendo ser tratada como uma correção de ordem superior nesses autoestados. Isso pode ser implementado fazendo
, autoestados da hamiltoniana fraca, não seriam autoestados de CP. Contudo, podemos argumentar que, como esta quebra de simetria é pequena, a diferença entre autoestados da hamiltoniana fraca e autoestados de CP deva ser muito pequena, podendo ser tratada como uma correção de ordem superior nesses autoestados. Isso pode ser implementado fazendo  e
e  em (39) e (40).
em (39) e (40).  é responsável por quantificar a intensidade de quebra de simetria CP e podem ser obtidos através da razão entre decaimentos que violam CP e aqueles que não violam. A análise dos dados para esses decaimentos resultam em (PDG)
é responsável por quantificar a intensidade de quebra de simetria CP e podem ser obtidos através da razão entre decaimentos que violam CP e aqueles que não violam. A análise dos dados para esses decaimentos resultam em (PDG)  para káons longos.n
para káons longos.nn
n
Leitura recomendada
n- n
- Capítulos 11 e 12 do livro “Introduction to Nuclear and Particle Physics”, Ashok Das e Thomas Ferbel.n
- Capítulo 4 do livro “Introduction to Elementary Particles”, David Griffths.n
Exercícios
n- n
- Qual é a reação conjugada de carga da reação
 ? Pode um sistema
? Pode um sistema  ser autoestado do operador de conjunção de carga? Discuta, de forma similar, a reação
ser autoestado do operador de conjunção de carga? Discuta, de forma similar, a reação  .n
.n
- Mostre que, em um caso não relativístico,
![[H,P]=0 [H,P]=0](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/60c4aca9d91076fa7dda4c18dea95ece.png) se o potencial de interação for par.n
se o potencial de interação for par.n
- Quais decaimentos são proibidos por invariância em carga:
 ,
,  ,
,  . Cheque o Particle Data Group para as propriedades destas partículas.n
. Cheque o Particle Data Group para as propriedades destas partículas.n
- Ignorando violação de CP, faça o gráfico da probabilidade de encontrar um anti-káon neutro em função do tempo, considerando que a amostra inicial era 100% pura de káons neutros.n
- Refaça o exercício anterior considerando que a amostra inicial é 100% pura de anti-kaons neutros.n
Deixe um comentário