Antipartículas, Klein-Gordon e Dirac

nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n

n
n
nO estudo de processos envolvendo partículas elementares é feito primordialmente através da medida de taxas com as quais determinado processo ocorre. A identificação da ocorrência de um determinado processo é feita através de várias técnicas experimentais distintas, observando as várias leis de conservação envolvidas, como visto anteriormente, por exemplo, no experimento CPLEAR para separar colisões onde são produzidos káons ou antikáons. As medidas dessas taxas, em geral, envolvem medidas de seções de choque. Em um experimento típico, um feixe de partículas colide sobre um alvo ou dois feixes de partículas colidem entre si, produzindo novas partículas. A taxa com que partículas são produzidas dependem das interações entre as partículas que colidem mas também dependem da frequência com a qual ocorrem as colisões. É muito comum, ao invés de se medir taxas de produção, medir sessões de choque, definida como:nn
n n n n n n

$\sigma = \frac{dN/dt}{\Phi}$

n nnonde dN/dt

corresponde à taxa de partículas de interesse medida e $\Phi$ corresponde ao fluxo de partículas incidentes. É fácil ver que a seção de choque tem unidade de área. A conexão entre o que se observa experimentalmente e o que se calcula teoricamente é feita através da relação entre taxas observadas e fluxos através de uma formulação teórica apropriada. Por exemplo, vamos tomar um sistema quântico não relativístico de partículas livres. Neste caso, partindo da relação E=p^2/2m

e utilizando os operadores adequados para energia e momento, chegamos à:nn
n n n n n n

$i\frac{\partial \psi}{\partial t} + \frac{1}{2m}\nabla^2 \psi = 0$

n nnTomando a equação acima, multiplicada por $-i\psi^*$ e somando seu C.C:nn
n n n n n n

$\left(i\frac{\partial \psi}{\partial t} + \frac{1}{2m}\nabla^2 \psi \right)(-i\psi^*) - \left(-i\frac{\partial \psi^*}{\partial t} + \frac{1}{2m}\nabla^2 \psi^* \right)(i\psi) = 0$

n nnchegamos facilmente à:nn
n n n n n n

$\frac{\partial (\psi^* \psi)}{\partial t} - \frac{i}{2m}(\psi^* \nabla^2\psi - \psi\nabla^2 \psi^*) = 0$

n nnLembrando que, nós podemos interpretar $(\psi^* \psi)=|\psi|^2=\rho$ como densidade de probabilidade, o que torna a equação acima muito similar à equação de continuidade:nn
n n n n n n

$\frac{\partial \rho}{\partial t} +\vec{\nabla}\vec{j} = 0$

n nnse definirmos a corrente de partículas:nn
n n n n n n

$\vec{j} = -\frac{i}{2m}(\psi^* \vec \nabla \psi - \psi \vec \nabla \psi^*)$

n nnou seja, é simples relacionar o lado teórico ao experimental conhecendo-se o fluxo de partículas de ambos os lados. Contudo, em física de partículas a situação nem sempre é simples como a exposta acima. É comum (ainda mais hoje em dia com aceleradores de altas energias) lidarmos com partículas em energias relativísticas, onde a eq. de Schrödinger, mostrada em (2) não se aplica. Outros problemas surgem, como antipartículas e spin, que não são previstos na mecânica quântica não relativística e são introduzidos empiricamente. Muito pode ser feito com a introdução de poucas ferramentas e alguns conceitos importantes. A construção da eq. (2) foi feita através da relação energia-momento para uma partícula não relativística livre. Vamos fazer o mesmo para o caso relativístico. Tomando a relação:nn
n n n n n n

n nncom:nn
n n n n n n

$E = i\frac{\partial}{\partial t} \text{ e } \vec{p} = -i\vec\nabla$

n nnpodemos chegar à:nn
n n n n n n

$-\frac{\partial^2\phi}{\partial t^2} +\nabla^2\phi = m^2\phi$

n nnque é conhecida como Equação de Klein-Gordon. Uma forma mais elegante de escrever a equação acima, se dá definindo o operador:nn
n n n n n n

$\square ^2 = \partial_\mu \partial^\mu \text{ com } \partial_\mu = \left ( \frac{\partial}{\partial t},\vec{\nabla} \right ) \text{ e } \partial^\mu = \left ( \frac{\partial}{\partial t},-\vec{\nabla} \right )$

n nnde modo que a Equação de Klein-Gordon pode ser escrita simplesmente como:nn
n n n n n n

$(\square ^2 +m^2)\phi = 0$

n nnDe forma similar ao que fizemos anteriormente, vamos tomar (9) e multiplicá-la por $-i\phi^*$ . O complexo conjugado de (9), multiplicamos por $-i\phi$ , chegando à:nn
n n n n n n

$i\phi^* \frac{\partial^2\phi}{\partial t^2} -i\phi^* \nabla^2\phi = -i\phi^* m^2\phi$

n nn
n n n n n n

$i\phi \frac{\partial^2\phi^*}{\partial t^2} -i\phi \nabla^2\phi^* = -i\phi^* m^2\phi$

n nnsubtraindo (13) de (12) obtém-se que:nn
n n n n n n

$\frac{\partial}{\partial t} \left[ i \left( \phi^* \frac{\partial \phi}{\partial t} - \phi \frac{\partial \phi^*}{\partial t} \right) \right]+\vec\nabla\left( -i(\phi^*\vec\nabla\phi -\phi\vec\nabla\phi^*)\right) = 0$

n nnComparando com (5) podemos, analogamente, definir:nn
n n n n n n

$\rho = i \left( \phi^* \frac{\partial \phi}{\partial t} - \phi \frac{\partial \phi^*}{\partial t} \right)$

n nn
n n n n n n

$\vec j = -i(\phi^*\vec\nabla\phi -\phi\vec\nabla\phi^*)$

n nnNo caso de uma partícula livre, a Equação de Klein-Gordon tem solução:nn
n n n n n n

$\phi = N e^{i(\vec p \vec x -Et)}$

n nnque, aplicando em (15) e (16) resulta em:nn
n n n n n n

$\rho = 2E|N|^2 \text{ e } \vec j = 2\vec p |N|^2$

n nnisto é, a densidade de probabilidade é proporcional ao módulo quadrático da constante de normalização

mas depende também da energia. No caso do sistema não relativístico (faça como exercício) não há dependência da energia. É bastante conveniente escrever (15) e (16) em uma forma de quadrivetor. Definimos o quadrivetor:nn
n n n n n n

$j^\mu = (\rho,\vec j) = i(\phi^*\partial^\mu \phi - \phi \partial^\mu \phi^*)$

n nne assim, a equação (14) toma uma forma bastante simples e elegante:nn
n n n n n n

$\partial_\mu j^\mu = 0$

n nnAlém disso, da equação (7) podemos escrever que:nn
n n n n n n

$E = \pm \sqrt{p^2 + m^2}$

n nno que gera resultados intrigantes. Para um dado valor de momento, a energia pode assumir valores positivos ou negativos. Isto gera ainda um enígma em (18), uma vez que a densidade de probabilidade pode ser negativa! Apesar de muito estranho, Dirac sugeriu que estes estados de energia negativa seriam uma primeira abordagem acerca de um universo ainda pouco explorado no início do séc. XX: antipartículas.nnAntipartículas (ou antimatéria) não era um conceito totalmente novo na época de Dirac. Em 1898, – Arthur Schuster (Nature, 1503, vol. 58, 367) escreveu um artigo (bastante interessante por sinal) sobre a possibilidade de existência de um outro tipo de matéria, que seria repelida gravitacionalmente da matéria ordinária que ele chamou de antimatéria. Neste artigo, o assunto é tratado quase como um conto de ficção, apenas ideias para pensar durante um feriado, como diz o autor. Dirac, em 1928, realmente tentou obter razão de uma possível solução para o problema de uma partícula relativística livre. A possibilidade de estados de energia negativos, e cada vez mais negativos, abaixo do limiar de E = -m

imposto em (21), faria com que partículas de energia positiva decaissem para estes estados cada vez mais negativos. Dirac então propôs uma solução onde todos os estados de energia negativa estariam populados por partículas (naquele momento, Dirac estava preocupado com a descrição relativística de elétrons), não havendo nenhum estado negativo livre. A observação destes elétrons nestes estados de energia negativa não seria possível. Isto previne que um elétron de energia positiva, observável, espontaneamente migrasse para estes estados de energia negativa por conta do princípio de exclusão de Pauli. Há um vazio de estados entre -m <e<m

. O que poderia ocorrer, na verdade, é que radiação externa (fótons por exemplo) acima do limiar entre os níveis negativos e positivos,

do elétron em (19) tornando:nn
n n n n n n

$j^\mu = -ie(\phi^*\partial^\mu \phi - \phi \partial^\mu \phi^*)$

n nnNeste caso, o termo j^0

é interpretado agora como uma densidade de carga e não mais uma densidade de probabilidade. Assim, assumir valores negativos deixa de ser um incomodo. Neste caso, j^0

assumiria valores negativos para elétrons reais e positivos para buracos. Stückelberg e Feynman, mais tarde, deram uma outra interpretação para os estados de energia negativa. Voltarei a isto mais tarde quando formos discutir um pouco diagramas de Feynman.nn
n
nHavia ainda um incômodo que fez Dirac repensar a Eq. de Klein Gordon: a Eq. de Klein-Gordon é uma equação de segunda ordem no tempo, ao contrário da Eq. de Schrödinger, que é de primeira ordem. Isto inclui uma condição de contorno a mais no problema para definir a evolução temporal de um estado. Esta foi uma das motivações de Dirac, encontrar uma forma de descrever sistemas quânticos relativísticos através de uma dependência de primeira ordem no tempo, algo similar à equação:nn
n n n n n n

$\hat H\psi = i\frac{\partial\psi}{\partial t}$

n nnSeja qual for a equação encontrada, esta deve respeitar todas as condições impostas pela relatividade. Em especial, esta equação deve satisfazer:nn
n n n n n n

$\hat H^2\psi = (\hat p^2 + m^2)\psi$

n nnDirac então assumiu uma forma geral para sua equação como sendo:nn
n n n n n n

$\hat H\psi = i\frac{\partial\psi}{\partial t} = \sum_{i}{\alpha_i \hat p_i \psi} + \beta m\psi$

n nnonde $\hat p_i$ são as componentes dos operadores de momento. Tomando o quadrado de $\hat H$ , temos:nn
n n n n n n

$\hat H^2\psi = \left(\beta^2 m^2 + \sum_{i}{\alpha_i^2 p_i^2} + \sum_i{(\alpha_i \beta +\beta \alpha_i)\hat p_i m} +(\alpha_i\alpha_j + \alpha_j\alpha_i)\hat p_i \hat p_j \right) \psi$

n nnonde o último termo na equação acima corresponde a todas as combinações $\alpha$ duas a duas. Para (26) satisfazer (24), $\alpha_i$ e $\beta$ devem satisfazer:nn
n n n n n n

$\alpha_i^2 = \beta^2 = 1$

n n
n n n n n n

$\alpha_i \beta +\beta \alpha_i = 0$

n n
n n n n n n

$\alpha_i\alpha_j + \alpha_j\alpha_i = 0$

n nnDe (27)-(29) percebe-se claramente que $\alpha_i$ e $\beta$ não podem ser números e sim matrizes. De (27) tiramos que estas matrizes sejam unitárias e seus autovalores sejam $\pm 1$ . Por conta das relações de anticomutação em (28) e (29), o traço dessas matrizes devem ser nulos. Como o traço das matrizes correspondem à soma dos seus autovalores, isto só é satisfeito se as matrizes tiverem dimensões pares. A menor matriz de dimensão par é a 2×2. O conjunto de matrizes 2×2 que satisfaz esta condição é o conjunto de matrizes de Pauli. Acontece que só temos 3 dessas matrizes e precisamos de 4 delas. Assim, a menor dimensão possível para as matrizes $\alpha_i$ e $\beta$ é 4×4. Há várias representações para estas matrizes e a mais comum é a representação de Dirac-Pauli, na forma:nn
n n n n n n

$\alpha_i = \begin{pmatrix}rn0 & \sigma_i\\ rn\sigma_i & 0 rn\end{pmatrix} \text{ e } rn\beta=\begin{pmatrix}rnI & 0\\ rn0 & -Irn\end{pmatrix}$

n nnonde $\sigma_i$ são as matrizes de Pauli, 2×2, e

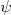são matrizes identidades de 2×2. Note que as matrizes acima são 4×4 mas normalmente se utiliza esta notação reduzida. Não confunda! Para (25) ser satisfeita, $\psi$ não pode ser uma função única. Ela deve apresentar uma forma vetorial, de quatro componentes. Escreve-se então que:nn
n n n n n n

$\psi=\begin{pmatrix}rn\psi_1\\ rn\psi_2\\ rn\psi_3\\ rn\psi_4rn\end{pmatrix}$

n nnEstes vetores de quatro componentes que satisfazem a equação de Dirac são chamados de espinores. Note que resolver (25) implica em resolver um sistema de 4 equações diferenciais acopladas umas às outras. Vamos ver agora como a eq. de Dirac (25) se comporta em termos de densidade de corrente e probabilidade. Definindo $\gamma^\mu = (\beta,\beta\alpha_1,\beta\alpha_2,\beta\alpha_3)$ vamos escrever (25) em termos de seus operadores diferenciais, multiplicando pela esquerda por $\beta$ (lembre-se que $\beta^2=1$ , passando os termos para o lado esquerdo, ou seja:nn
n n n n n n

$i\gamma^0 \frac{\partial\psi}{\partial t} + i\sum_{i}{\gamma_i \frac{\partial \psi}{\partial x_i}} - m\psi = 0$

n nnQue podemos escrever, como:nn
n n n n n n

$i\gamma^\mu \partial_\mu \psi - m\psi = 0$

n nnque é conhecida como a forma covariante da equação de Dirac. Vamos agora encontrar a equação da continuidade para um sistema que obedeça a equação de Dirac. Como estamos lidando com matrizes, ao invés de complexo conjugado, devemos tratar de hermitianos conjugados. O hermitiano conjugado de (32) é, lembrando que $\gamma^0^\dagger = \gamma^0$ e $\gamma^i^\dagger = -\gamma^i$ :nn
n n n n n n

$-i \frac{\partial\psi^\dagger}{\partial t}\gamma^0 -i\sum_{i}{\frac{\partial \psi^\dagger}{\partial x_i}(-\gamma_i)} + m\psi^\dagger$

n nnPara sumir com o sinal de menos no termo da somatória, vamos multiplicar pela direita por $\gamma^0$ , sabendo que $\gamma^i \gamma^0 = -\gamma^0 \gamma^i$ , de modo que:nn
n n n n n n

$-i \frac{\partial\psi^\dagger}{\partial t}\gamma^0 \gamma^0 -i\sum_{i}{\frac{\partial \psi^\dagger}{\partial x_i}\gamma^0 \gamma_i} + m\psi^\dagger \gamma^0$

n nnDefinindo $\bar{\psi} = \psi^\dagger \gamma^0$ podemos escrever a equação acima como:nn
n n n n n n

$i\partial_\mu \bar{\psi} \gamma^\mu + m\bar{\psi} = 0$

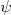n nnSe multiplicarmos (33) pela esquerda por $\bar{\psi}$ e (36) pela esquerda por $\psi$ e somarmos os resultados, obtemos:nn
n n n n n n

$\bar{\psi}\gamma^\mu (\partial_\mu \psi) + (\partial_\mu \bar{\psi})\gamma^\mu \psi = 0$

n nnDefinindo $\j^\mu = \bar{\psi}\gamma^\mu \psi$ é fácil ver que $\partial_\mu j^\mu$ vale:nn
n n n n n n

$\partial_\mu j^\mu = \bar{\psi}\gamma^\mu (\partial_\mu \psi) + (\partial_\mu \bar{\psi})\gamma^\mu \psi$

n nnDe modo que (37) equivale à:nn
n n n n n n

$\partial_\mu j^\mu = 0$

n nnQue é a equação da continuidade. Podemos ver que o primeiro termo da equação, j^0

vale:nn
n n n n n n

$j^0 = \bar{\psi}\gamma^0 \psi = \psi^\dagger \gamma^0 \gamma^0 \psi = \psi^\dagger \psi = |\psi|^2$

n nnonde podemos notar claramente o termo da densidade de probabilidade que, nesta formulação, acaba tendo a mesma interpretação que obtivemos na versão não relativística, em (4).
n
nPodemos re-escrever o quadrivetor para a corrente de probabilidade de carga como sendo:nn
n n n n n n

$j^\mu = -e\psi^\dagger \gamma^\mu \psi$

n nno termo

foi inserido para retomar a definição de Pauli-Weisskopf, como no caso da Eq. de Klein-Gordon.
n
nVamos olhar as soluções da eq. de Dirac para partículas livres. Retomando da equação (25) vamos escrever:nn
n n n n n n

$H\psi = i\frac{\partial\psi}{\partial t} = (\vec \alpha \cdot \vec p + \beta m)\psi = (-i \vec \alpha \cdot \vec \nabla + \beta m)\psi = E\psi$

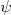n nnonde o produto escalar representa acima, para simplificar a notação, representa a somatória das matrizes com as componentes do operador momento. $\psi$ é dado por (31). Para partículas livres, vamos olhar soluções do tipo $\psi(\vec r,t) = \psi(\vec r) e^{-iEt}$ onde $\psi(\vec r)$ é um espinor de 4 componentes. Como $[H,\vec p]=0$ , podemos também achar funções que sejam autoestados de momento. Deste modo, vamos escrever que $\psi(\vec r) = u_p e^{i\vec p \cdot \vec r}$ , sendo u_p

também um espinor de 4 componentes. Após estas substituições a eq. (39) fica simplesmente:nn
n n n n n n

$(\vec\alpha\cdot\vec p +\beta m)u_p = E u_p$

n nnComo as matrizes $\alpha$ são compostas de blocos de 2×2 bem isoladas, podemos escrever u_p

como sendo um vetor de dois estados onde cada estado é um vetor também de dois estados. Isto facilita encontrar as soluções para u_p

. Assim, por simplicidade, escrevemos que:nn
n n n n n n

$u_p=\begin{pmatrix}rn\phi_p\\ rn\chi_p rn\end{pmatrix}$

n nne, deste modo podemos escrever (43) na forma matricial:nn
n n n n n n

$\begin{pmatrix}rnm & \vec\sigma\cdot\vec p \\ rn\vec\sigma\cdot\vec p & -m rn\end{pmatrix}\begin{pmatrix}rn\phi_p\\ rn\chi_p rn\end{pmatrix} = rn\begin{pmatrix}rnE &0 \\ rn0 &E rn\end{pmatrix} \begin{pmatrix}rn\phi_p\\ rn\chi_p rn\end{pmatrix}$

n nnQue pode ser trabalhada, resultando nas equações:nn
n n n n n n

$(E-m)\phi_p -\vec\sigma\cdot\vec p \chi_p = 0$

n nn
n n n n n n

$-\vec\sigma\cdot\vec p \phi_p + (E+m)\chi_p = 0$

n nnDestas equações, podemos escrever $\chi_p$ em função de $\phi_p$ , o que resulta em:nn
n n n n n n

$\chi_p = \frac{\vec\sigma\cdot\vec p}{E+m}\phi_p$

n nnque, subtituindo acima e lembrando que $(\vec\sigma\cdot\vec p)^2 = p^2$ , resulta em:nn
n n n n n n

$(E^2 - (m^2 + p^2))\phi_p = 0$

n nnCujas soluções são tais que $E = \pm \sqrt{p^2 + m^2}$ ou seja, os mesmos estados de energia que os obtidos na Eq. de Klein-Gordon. Vamos agora obter os autoestados destes autovalores. Note que, como a hamiltoniana é uma matriz de quatro dimensões, temos dois autoestados de energia positiva e dois autoestados de energia negativa.
n
nPara $\phi_p=\begin{pmatrix}rn1\\ rn0rn\end{pmatrix}\text{ ou }\begin{pmatrix}rn0\\ rn1rn\end{pmatrix}$ n n n
n nne sabendo que:nn
n n n n n n

$\vec\sigma\cdot\vec p = \begin{pmatrix}rnp_3 & p_1 - ip_2\\ rnp_1+ip_2 & -p_3 rn\end{pmatrix}$

n nnresulta em:nn
n n n n n n

$\chi_p = \begin{pmatrix}rnp_3/(E+m)\\ rn(p_1+ip_2)/(E+m)rn\end{pmatrix}\text{ ou }\begin{pmatrix}rn(p_1-ip_2)/(E+m)\\ rn-p_3/(E+m)rn\end{pmatrix}$

n nnou seja:nn
n n n n n n

$u_p = \begin{pmatrix}rn1\\rn0\\rnp_3/(E+m)\\ rn(p_1+ip_2)/(E+m)rn\end{pmatrix}\text{ ou }\begin{pmatrix}rn0\\rn1\\rn(p_1-ip_2)/(E+m)\\ rn-p_3/(E+m)rn\end{pmatrix}$

n nnVamos olhar dois limites que podem nos dizer muita coisa a respeito destes estados de energia positiva. Primeiramente, o limite $p\rightarrow 0$ . Neste caso, as funções de onda, voltando todo o caminho até $\psi(\vec r,t)$ , tomam a forma:nn
n n n n n n

$\psi(t)=\begin{pmatrix}rn1\\ rn0\\ rn0\\ rn0rn\end{pmatrix} e^{-imt}\text{ e }\psi(t)=\begin{pmatrix}rn0\\ rn1\\ rn0\\ rn0rn\end{pmatrix} e^{-imt}$

n nnque correspondem a partículas de energia positiva propagando no tempo. Temos dois estados para estas partículas que também são autovalores das matrizes de Pauli. Então cada um destes autoestados correspondem a um dos estados de uma partícula de spin 1/2. Agora vamos tomar a situação de que $p\sim E$ . Vamos escolher como sistema de referência o eixo 3, de modo que p_1=p_2=0

. Assim, os autoestados de energia positiva neste limite tornam-se:nn
n n n n n n

$\psi(z,t)=\begin{pmatrix}rn1\\ rn0\\ rn1\\ rn0rn\end{pmatrix} e^{ipz}e^{-iEt}\text{ e }\psi(t)=\begin{pmatrix}rn0\\ rn1\\ rn0\\ rn-1rn\end{pmatrix} e^{ipz}e^{-iEt}$

n nnNote que, novamente temos dois auoestados com diferentes espinores. A escolha de movimento positivo no eixo-z indica que no primeiro autoestado o spin estaria alinhado com a direção z do momento e no segunto, anti-alinhado com este momento.
n
nOs autoestados de energia negativa podem ser construídos de forma análoga, agora tomando:nn
n n n n n n

$\chi_p=\begin{pmatrix}rn1\\ rn0rn\end{pmatrix}\text{ ou }\begin{pmatrix}rn0\\ rn1rn\end{pmatrix}$

n nne resolvendo para $\phi_p$ . Os resultados são similares aos obtidos para partículas de energia positiva (façam como exercício). Porém, um detalhe que aparece nestas soluções é que a dependência temporal dos espinores toma a forma:nn
n n n n n n

$\psi(t)\rightarrow e^{im|E|t}$

n nnque tem sinal oposto ao obtido em (55). Vocês se lembram que, lá atrás, eu mencionei que Stückelberg e Feynman deram uma interpretação diferente da de Dirac para os estados de energia negativa. Eles argumentaram que estes estados de energia negativa seria o equivalente a uma partícula que se propaga para trás no tempo, como aparece nas soluções para os autoestados de energia negativa. A analogia com o buraco de Dirac aparece quando na analogia de que uma antiparticula de energia positiva (o buraco de Dirac no estado de energia negativa) equivale a uma partícula de energia negativa andando para trás no tempo. Este conceito vai ser muito importante quando formos discutir diagramas de Feynman. n
n
nn

Apêndice

nnVamos mostrar que as definições para os 4-vetores gradientes têm a notação invertida a de 4-vetores tradicionais, como apresentada em (10). Inicialmente, podemos escrever que:nn
n n n n n n

$x_\mu = g_{\nu\mu} x^\nu$

n nnDiferenciando ambos os lados temos:nn
n n n n n n

$\partial x_\mu = g_{\nu\mu} \partial x^\nu$

n nnO que resulta em:nn
n n n n n n

$g_{\nu\mu} = \frac{\partial x_\mu}{\partial x^\nu}$

n nnAgora vamos tomar um campo escalar qualquer $\phi$ e calcular as componentes do seu quadrigradiente, ou seja $\frac{\partial \phi}{\partial x^\nu}$ . Usando a regra da cadeia, temos:nn
n n n n n n

$\frac{\partial \phi}{\partial x^\nu} = \frac{\partial \phi}{\partial x_\mu} \frac{\partial x_\mu}{\partial x^\nu}$

n nnSendo assim:nn
n n n n n n

$\frac{\partial \phi}{\partial x^\nu} = g_{\nu\mu} \frac{\partial \phi}{\partial x_\mu}$

n nnNote que as componentes do quadrigradiente em (59) se transformam da mesma forma de um quadrivetor qualquer, como em (55), com a diferença de que as notações de covariante e contravariante são invertidas, justificando a notação em (10).nn

Leitura recomendada

Capítulos 3 e 5 do livro “Quarks e Leptons: an introductory course in modern particle physics”, Francis Halzen e Alan D. Martinn
Capítulos 1, 2 e 3 do livro “Relativistic Quantum Mechanics”, Bjorken e Drell.n
Começo do capítulo 7 do livro “Introduction to elementary particles”, David griffths.n

n
n

Exercícios

Mostre que $\alpha_i$ e $\beta$ são hermitianas, de traço nulo com autovalores $\pm 1$ .n
Mostre que cada uma das 4 componentes de um espinor que satisfaça a eq. de Dirac também satisfaz a eq. de Klein-Gordon. n
Encontre os espinores para antipartículas, isto é, para os autoestados de energia negativa. Mostre que estes espinores são os mesmos para as partículas trocando os sinais de energia e momento.n
É comum utilizar a notação cortada, por exemplo, $\not p$ , onde $\not a = \gamma^\mu a_\mu$ . Mostre que $\not p \not p = p^2$ . n
Mostre que $\sum_{s=1,2}{u^{(s)}\bar{u}^{(s)}} = \not p +m$ onde $u^{(s)}$ , com são os dois espinores para estados de partículas.n
Mostre que $\sum_{s=1,2}{v^{(s)}\bar{v}^{(s)}} = \not p -m$ onde $v^{(s)}$ , com são os dois espinores para estados de antipartículas.n
Mostre que $\bar u^{(s)}u^{(s)}=2m$ e que $\bar v^{(s)}v^{(s)}=-2m$ n
Definindo $\gamma^5=i\gamma^0\gamma^1\gamma^2\gamma^3$ , mostre que $(\gamma^5)^2 = I$ , $\gamma^{5\dagger} = \gamma^5$ e $\gamma^5\gamma^\mu + \gamma^\mu\gamma^5 = 0$ .nn

]]>

Antipartículas, Klein-Gordon e Dirac

Apêndice

Leitura recomendada

Exercícios

Deixe um comentário Cancelar resposta