nnVersão para impressãon
nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n
nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
n
 . O estudo das partículas que emergem desta reação permite inferir propriedades do próton, quem são seus constituintes e como seus constituintes interagem entre si. Da mesma forma, o decaimento de uma partícula, como já fizemos no caso do káon, permite explorar significativamente as interações fundamentais que geram este decaimento. O que há de comum nestes processos todos é que o sistema, durante um intervalo de tempo finito, interage com algum campo de modo a alterar sua configuração para outro estado qualquer. O cálculo de taxas de decaimento, probabilidades e seções de choque é decorrente, então, do entendimento de como a interação de um estado com este campo pode altera-lo a evoluir de outra maneira. Há diversas formas de se explorar este problema. Podemos utilizar teorias de espalhamento, cálculos complexos de evoluções temporais ou, como veremos aqui, teoria de perturbação. Este último, requer que, de alguma maneira, como o próprio nome sugere, esta interação com um campo externo seja pequena, de modo que o efeito prático seja apenas o de perturbar o estado inicial do sistema. O resultado da implementação de métodos perturbativos quânticos em física de partículas é o que conhecemos hoje como diagramas de Feynman, que leva o nome de seu idealizador e, como veremos, consiste em um conjunto de regras gráficas para fazer cálculos de seções de choque e taxas de decaimentos através de teoria de perturbação. Apesar de ser um método prático bastante poderoso e simples, que desenvolve uma enorme intuição sobre as interações que ocorrem em um determinado processo físico, ainda há grupos de cientistas que renegam o seu uso. Contudo, se você for seguir a carreira de física de partículas será praticamente impossível nunca desenhar um desses diagramas em uma conversa no café com um colega.n
. O estudo das partículas que emergem desta reação permite inferir propriedades do próton, quem são seus constituintes e como seus constituintes interagem entre si. Da mesma forma, o decaimento de uma partícula, como já fizemos no caso do káon, permite explorar significativamente as interações fundamentais que geram este decaimento. O que há de comum nestes processos todos é que o sistema, durante um intervalo de tempo finito, interage com algum campo de modo a alterar sua configuração para outro estado qualquer. O cálculo de taxas de decaimento, probabilidades e seções de choque é decorrente, então, do entendimento de como a interação de um estado com este campo pode altera-lo a evoluir de outra maneira. Há diversas formas de se explorar este problema. Podemos utilizar teorias de espalhamento, cálculos complexos de evoluções temporais ou, como veremos aqui, teoria de perturbação. Este último, requer que, de alguma maneira, como o próprio nome sugere, esta interação com um campo externo seja pequena, de modo que o efeito prático seja apenas o de perturbar o estado inicial do sistema. O resultado da implementação de métodos perturbativos quânticos em física de partículas é o que conhecemos hoje como diagramas de Feynman, que leva o nome de seu idealizador e, como veremos, consiste em um conjunto de regras gráficas para fazer cálculos de seções de choque e taxas de decaimentos através de teoria de perturbação. Apesar de ser um método prático bastante poderoso e simples, que desenvolve uma enorme intuição sobre as interações que ocorrem em um determinado processo físico, ainda há grupos de cientistas que renegam o seu uso. Contudo, se você for seguir a carreira de física de partículas será praticamente impossível nunca desenhar um desses diagramas em uma conversa no café com um colega.nn
nSeja um sistema quântico definido por um estado
 , superposição de auto-estados do Hamiltoniano
, superposição de auto-estados do Hamiltoniano  . Se, em determinado momento, um potencial
. Se, em determinado momento, um potencial 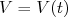 , dependente do tempo, é aplicado ao sistema, o Hamiltoniano, durante o tempo em que esse potencial atua, é modificado e vale:nn
, dependente do tempo, é aplicado ao sistema, o Hamiltoniano, durante o tempo em que esse potencial atua, é modificado e vale:nnn
 |
n
n
 deixa de ter uma evolução temporal trivial. Quando esse potencial deixa de agir, a configuração do estado evoluído pode ser tal que ele se encontre em um estado
deixa de ter uma evolução temporal trivial. Quando esse potencial deixa de agir, a configuração do estado evoluído pode ser tal que ele se encontre em um estado  , diferente do inicial. Um exemplo de um potencial desse tipo pode ser uma perturbação devido à radiação eletromagnética ou uma perturbação de natureza fraca, responsável pelo decaimento β de um núcleo. Esperamos que esse potencial seja de natureza perturbativa e que atue em um intervalo finito de tempo. Desse modo, podemos usar teoria de perturbações dependentes do tempo para determinar como é a evolução do sistema.nn
nPara descrever esse problema, vamos iniciar supondo o conhecimento do Hamiltoniano não perturbado,
, diferente do inicial. Um exemplo de um potencial desse tipo pode ser uma perturbação devido à radiação eletromagnética ou uma perturbação de natureza fraca, responsável pelo decaimento β de um núcleo. Esperamos que esse potencial seja de natureza perturbativa e que atue em um intervalo finito de tempo. Desse modo, podemos usar teoria de perturbações dependentes do tempo para determinar como é a evolução do sistema.nn
nPara descrever esse problema, vamos iniciar supondo o conhecimento do Hamiltoniano não perturbado,  e todos os seus auto-estados
e todos os seus auto-estados  , de modo que:nn
, de modo que:nnn
 |
n
n
 , já que esses formam uma base ortonormal. Assim, em
, já que esses formam uma base ortonormal. Assim, em  o estado quântico pode ser descrito como:nn
o estado quântico pode ser descrito como:nnn
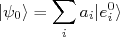 |
n
n
n
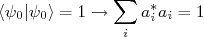 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
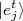 , sabendo que
, sabendo que 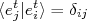 , temos:nnn
, temos:nnnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
 pode ser pequeno e, consequentemente, tratado como uma perturbação. Nesse caso, teoria de perturbação pode ser utilizada para desacoplar as várias equações, tornando a resolução do sistema mais simples.n
nnPara resolver perturbativamente a eq. (13) podemos expandir as constantes
pode ser pequeno e, consequentemente, tratado como uma perturbação. Nesse caso, teoria de perturbação pode ser utilizada para desacoplar as várias equações, tornando a resolução do sistema mais simples.n
nnPara resolver perturbativamente a eq. (13) podemos expandir as constantes  de modo que:nn
de modo que:nnn
 |
n
n
n
nUma forma alternativa, mais simples de compreender, envolve repensar um pouco o que fizemos até agora. Vamos trabalhar com a interpretação de Dirac para evolução de estados. Esta é uma interpretação intermediária entre a de Schrödinger, na qual os operadores são estáticos no tempo e o estado evolui no tempo e a de Heinsemberg, onde os estados são estáticos e os operadores evoluem no tempo. Nesta situação, tanto estados como operadores evoluem no tempo. Neste caso, definimos um estado, em um instante qualquer de tempo, nesta interpretação (subscrito I) em relação à interpretação de Schrödinger (subscrito S) como:nn
n
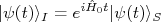 |
n
n
n
 |
n
n
 . Vamos agora definir como o estado, nesta interpretação, evolui, se sujeito à ação de uma hamiltoniana como a descrita em (1). Neste caso:nn
. Vamos agora definir como o estado, nesta interpretação, evolui, se sujeito à ação de uma hamiltoniana como a descrita em (1). Neste caso:nnn
 |
n
n
n
 |
n
n
 , de modo que:nn
, de modo que:nnn
 |
n
n
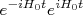 entre o potencial e o estado, temos:nn
entre o potencial e o estado, temos:nnn
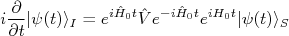 |
n
n
n
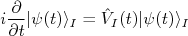 |
n
n
 em termos de uma base de autoestados de
em termos de uma base de autoestados de  vamos escrever que a evolução temporal do estado é resultado da ação de um operador (operador de evolução temporal) no estado inicial. Assim, definimos, na interpretação de Dirac:nn
vamos escrever que a evolução temporal do estado é resultado da ação de um operador (operador de evolução temporal) no estado inicial. Assim, definimos, na interpretação de Dirac:nnn
 |
n
n
 , que pode ser zero. Substituindo (38) em (37):nn
, que pode ser zero. Substituindo (38) em (37):nnn
 |
n
n
n
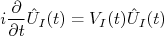 |
n
n
 , chegamos em:nn
, chegamos em:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
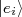 , como na equação (3), onde todos coeficientes da expansão, exceto um deles, são nulos. Em um instante de tempo qualquer, o estado do sistema é então descrito como:nn
, como na equação (3), onde todos coeficientes da expansão, exceto um deles, são nulos. Em um instante de tempo qualquer, o estado do sistema é então descrito como:nnn
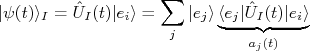 |
n
n
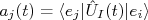 . Comparando esta expressão com (15) e utilizando a expansão para o operador de evolução temporal, em (44), lembrando que
. Comparando esta expressão com (15) e utilizando a expansão para o operador de evolução temporal, em (44), lembrando que  , é fácil ver que os termos
, é fácil ver que os termos  podem ser dados por:nn
podem ser dados por:nnn
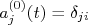 |
n
n
n
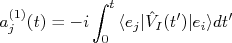 |
n
n
n
 |
n
n
n
 |
n
n
 é dado por:nn
é dado por:nnn
 |
n
n
 . O termo de ordem 0 indica que o sistema não sofre alteração e, por conta disso permanece inalterado. O termo de ordem 1 indica que ha uma única interação com o potencial. No termo de ordem 2, há uma interação com o potencial, o sistema evolui um pouco mais e há uma segunda interação com o potencial e assim sucessivamente. Estes termos podem ser representados visualmente na figura 1.n
. O termo de ordem 0 indica que o sistema não sofre alteração e, por conta disso permanece inalterado. O termo de ordem 1 indica que ha uma única interação com o potencial. No termo de ordem 2, há uma interação com o potencial, o sistema evolui um pouco mais e há uma segunda interação com o potencial e assim sucessivamente. Estes termos podem ser representados visualmente na figura 1.nn
n

nFigura 1 – Representação dos termos da expansão perturbativa.n
n
n
n
n
Leitura recomendada
n- n
- Capítulo 3 do livro “Quarks e Leptons: an introductory course in modern particle physics” Francis Halzen e Alan D. Martinn
- Capítulo 5 do livro “Modern Quantum Mechanics”, J. J. Sakurain
Exercícios
n- nn
- Sendo um potencial do tipo
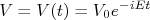 mostre, no limite de tempo tendendo a infinito, que, em primeira ordem de teoria de pertubações dependente do tempo,
n
mostre, no limite de tempo tendendo a infinito, que, em primeira ordem de teoria de pertubações dependente do tempo,
n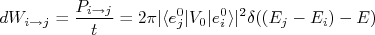
n
nonde é a probabilidade de encontrar um estado j, sabendo que o sistema encontra-se, no tempo inicial, no estado i. Esta expressão é conhecida como Regra de Ouro de Fermi.n
é a probabilidade de encontrar um estado j, sabendo que o sistema encontra-se, no tempo inicial, no estado i. Esta expressão é conhecida como Regra de Ouro de Fermi.n
- Calcule, para o mesmo potencial do exercício anterior,
 para o termo de segunda ordem. Discuta o resultado.n
para o termo de segunda ordem. Discuta o resultado.n
Deixe um comentário