Diagramas de Feynman e uma discussão qualitativa das interações

nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n

n
nEm física de partículas as interações são descritas através da troca de uma partícula mediadora de interação. Pode-se interpretar que a interação se dá por uma troca de partículas onde se requer que leis de conservação de momento sejam respeitadas. No eletromagnetismo, por exemplo, as interações são realizadas à distância e podem ser explicadas através das equações de Maxwell. Já na QED (Eletrodinâmica Quântica), teoria quântica de campos para o eletromagnetismo, estas interações são descritas através da troca de fótons entre as partículas. Na QCD (Cromodinâmica Quântica), temos as trocas de glúons como responsáveis pelas interações entre as partículas com carga de cor. Nas interações fracas, são os bósons W e Z, os responsáveis pelas interações.
n
nUm exemplo típico deste mecanismo de interação é a interação entre duas cargas. Um elétron, por exemplo, pode ser descrito como uma partícula com seu campo coulombiano. Podemos interpretar que este campo consiste em emissões de fótons pelo elétron que são rapidamente reabsorvidos. A emissão de um fóton faz com que uma parcela da energia do elétron seja emprestada a este fóton. Há problemas sérios de conservação de energia neste esquema, a menos que o fóton exista por um período de tempo compatível com o princípio da incerteza, $\Delta E \Delta t \sim 1$ . Fótons muito energéticos existem por um intervalo de tempo muito curto. Na presença de outra carga neste campo, pode ocorrer de este fóton não ser reabsorvido mas, ao invés disso, ser absorvido pela outra carga. Neste caso, o momento e energia deste fóton seria transferido da sua carga de origem para a carga de destino e, esta transferência seria responsável pela repulsão ou atração entre as cargas. O fato de o fóton ter existido por um intervalo de tempo curto, apenas para realizar a interação entre as duas cargas faz com que nós o chamemos de “virtual”. Por ser uma partícula que existe por um intervalo de tempo muito pequeno, da ordem da escala da interação, elas não podem ser observadas. Já vimos que, em relatividade, a relação entre energia e momento se dá de forma que m^2=E^2-p^2

, onde

é a massa invariante da partícula. Por conta das relações de incerteza, partículas virtuais podem receber momento e energia que não respeitam esta relação, ou seja $E^2-p^2 \ne m^2$ . Muitos interpretam isso como sendo uma violação da conservação de energia para partículas virtuais. Muitos (eu incluído) preferem interpretar que a partícula virtual pode ser emitida com uma massa diferente daquela que ela teria se fosse uma partícula real. Neste caso, um fóton virtual pode ser massivo. Estas partículas, que possuem massas diferentes das “tabeladas” são normalmente denominadas de “off-shell” (fora da prateleira ????) enquanto as partículas com massa iguais às observadas são chamadas de “on-shell” (na prateleira ????).
n
nAlguém pode argumentar que esta descrição para interações entre partículas tem uma falha: ela só prevê repulsão. Se a partícula mediadora sai de uma carga em direção à outra, carregando momento, a física clássica nos sugere, automaticamente, que a carga da qual ela foi emitida recuaria. Assim que esta partícula mediadora fosse absorvida pela outra carga, a transferência de momento faria com que esta outra carga fosse repelida. É a ideia clássica de dois patinadores lançando uma bola de um para o outro. Nesta visão, os patinadores se distanciam um do outro. Acontece que, em teoria quântica de campos, o sentido do momento carregado pela partícula mediadora não necessariamente deve seguir as restrições clássicas. Ou seja, o impulso fornecido carrega um sinal que faz com que as partículas se atraiam ou se afastem, dependendo deste sinal. Em linhas gerais, a propagação de partículas virtuais é diferente da propagação de partículas reais e, por conta disso a visão clássica não se aplica.n
n
nCom a noção de que interações correspondem a troca de partículas e com o conhecimento de que uma transição de um estado para outro pode (em circunstâncias especiais que se aplicam bem à QED) ser descrita por uma expansão perturbativa, Feynman introduziu uma forma bastante simples e elegante de calcular transições e de representar graficamente interações e processos físicos envolvendo partículas: os diagramas de Feynman. Feynman desenvolveu um conjunto de receitas (regras de Feynman) que permitem calcular a contribuição de processos físicos em qualquer ordem da expansão perturbativa. Apesar de ser uma ferramenta extremamente poderosa e conveniente, os diagramas não são unanimidade. Mesmo assim, constituem uma forma gráfica extremamente conveniente, até para aqueles que não utilizam estas técnicas para calcular transições.n
n
nUm diagrama de Feynman consiste na representação espaço-temporal de um processo físico qualquer em um diagrama bi-dimensional. No eixo horizontal, em geral, representa-se a variável temporal. No eixo vertical, representa-se as grandezas espaciais. Cada diagrama, que representa um termo de uma série perturbativa, é composto de vértices (nem sempre explicitamente desenhados, mas facilmente identificáveis) e linhas, ligadas a estes vértices. O sistema evolui da esquerda para a direita, assim como o tempo. As linhas representam as partículas e são desenhadas como flechas que evoluem do passado para o presente, isto é, avançam no tempo. Antipartículas, como já discutimos anteriormente, são representadas como flechas que evoluem do futuro para o passado, em sentido contrário às partículas. Bósons, em geral, são representados por outras formas. Por exemplo, um fóton é normalmente representado como uma espécie de “onda” e um glúons, como um tipo de mola. Outros bósons, como o W e Z, podem ser representados como linhas tracejadas, embora se encontrem diagramas com outros layouts. Isso não é muito problemático, uma vez que é comum se colocar legendas nas linhas para facilitar a interpretação da informação.
n
nNa figura 1 vemos um exemplo de um diagrama de Feynman onde um elétron emite espontaneamente um fóton. Apesar de já termos visto que este processo não ocorre espontaneamente, logo percebemos que, nas interações eletromagnéticas, este é o bloco básico para descrição dos fenômenos de interação: uma carga emite um fóton que pode ser absorvido por outra carga.n
n
nn

nFigura 1 – Exemplo de um diagrama de Feynman.n
n
n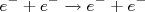nPor exemplo, a reação de espalhamento $e^- + e^- \rightarrow e^- + e^-$ entre dois elétrons pode ser facilmente descrita, em um diagrama de Feynman, por (figura 2):n
n
n

nFigura 2 – Espalhamento entre dois elétrons.
n
nnOu seja, há uma troca de um fóton virtual entre os dois elétrons. Em QED, este processo é chamado de espalhamento de Moller. Os vértices representam o ponto de emissão/absorção deste fóton. É irrelevante saber quem emitiu ou quem absorveu o fóton neste caso. É por conta disso que o fóton é representado verticalmente. O processo acima representa a repulsão entre duas cargas. Um processo simples envolvendo partículas e antipartículas pode ser obtido simplesmente girando o diagrama da figura 2 de 90^o, como o mostrado na figura 3. Um par elétron-pósitron se aniquila formando um fóton (virtual) que, mais tarde, se converte em outro par elétron pósitron. Este processo, em QED, é chamado de espalhamento de Bhabha. Esta é uma das formas de representar o espalhamento $e^+ + e^- \rightarrow e^+ + e^-$ e é também uma das representações da atração coulombiana.
n
n

nFigura 3 – Uma das repsesentações do espalhamento elétron pósitron.
n
nnComo fazemos a correlação entre os diagramas de Feynman e o cálculo de uma transição de estados? Lembrando, a série de Dyson que deduzimos anteriormente para uma expansão perturbativa foi:nn
n n n n n n

$a_i(t) = a_i^{(0)}+a_i^{(1)}+a_i^{(2)}+a_i^{(3)}+...$

n nncom:nn
n n n n n n

$a_j^{(0)}(t) = \delta_{ji}$

n n
n n n n n n

$a_j^{(1)}(t) = - i \int_{0}^{t}{\langle e_j|\hat V_I(t$

n n
n n n n n n

$a_j^{(2)}(t) = -i^2 \int_{0}^{t}{\int_{0}^{t$

n nne assim por diante. Note que, em (2), não há nenhuma alterando o estado inicial, ou seja, o termo de ordem zero é equivalente a não sofrer interação. Em (3), há apenas uma interação. A ordem de um diagrama de Feynman está então relacionada ao número de interações presentes. Por exemplo, os diagramas das figuras 2 e 3 são de primeira ordem, há apenas uma interação entre as partículas. Na figura 4 mostramos alguns diagramas de segunda e terceira ordem. 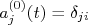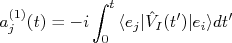Note que, mesmo havendo duas interações, nem sempre estas interações se dão entre as duas partículas reais que participam do processo.n
n
nn

nFigura 4 – Exemplos de diagramas de segunda e terceira ordem.
n
nnnnPode-se notar que diversos processos em QED podem ser construídos a partir do bloco básico mostrado na figura 1. Com este bloco básico podemos construir, por exemplo, diagramas para aniquilação elétron-pósitron, produção de pares e espalhamento Compton, conforme mostrados na figura 5. n
n
nn

nFigura 5 – Outros processos básicos na QED.
n
nnnNote que, comparando os diagramas das figuras 3 e 4 que eles representam o mesmo observável físico, ou seja, o espalhamento entre elétron e pósitron, cada um correspondendo a um termo da série perturbativa. Neste caso, o cálculo final para um determinado processo observável deve levar em consideração a contribuição de todos os possíveis diagramas que possuem os mesmos estados iniciais e finais, em todas as ordens. Isto está representado na figura 6. Alguém pode argumentar que é possível construir infinitos diagramas para um processo simples como este. Sim, é possível. Acontece que, por ser uma representação de uma série perturbativa, espera-se que esta série seja convergente. No caso da QED, cada vértice contribui com um fator $\alpha = 1/137$ . Como este número é menor que 1, diagramas com muitos vértices contribuem muito pouco para o resultado final. Isto nem sempre acontece, por exemplo, na QCD, que torna-se perturbativa somente em situações bem determinadas.n
n
nn

nFigura 6 – Alguns termos que contribuem para o espalhamento elétron + pósitron.nn
n
nnApesar de estarmos utilizando elétrons e pósitrons para construir alguns diagramas para interações eletromagnéticas, estes mesmos diagramas se estendem para para partículas que possuam cargas elétricas como quarks, múons, etc. Por exemplo, um diagrama que descreva o decaimento do píon neutro ( 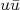$u\bar{u}$ ) em dois fótons $\pi^0 \rightarrow \gamma + \gamma$ pode ser construído como o mostrado na figura 7.n
n
nn

nFigura 7 – Um possível diagrama para o decaimento do píon neutro.nn
n
nnDepois desta discussão sobre diagramas de Feynman para QED, antes de discutir um pouco sobre QCD e interações fracas, vamos olhar um elétron livre sobre este ponto de vista. A emissão/absorção dos seus fótons virtuais foi comentada anteriormente. Um elétron não é apenas um elétron. Ele é uma estrutura complicada. Acontece que estes fótons virtuais podem converter em pares elétron-pósitron também virtuais, em uma cascata enorme, como esquematizado na figura 8. Acontece que, como mostrado na figura 8, nestes pares virtuais, por conta da carga negativa do elétron, o pósitron virtual tende a ficar mais próximo do elétron do que o elétron virtual. Assim, o elétron é cercado por uma nuvem de cargas elétricas onde as cargas positivas estão mais próximas que as negativas. Sendo assim esta nuvem é polarizada. Um esquema de como seria a distribuição de cargas, neste contexto, é mostrado na figura 9. Este fenômeno faz com que a medida da carga elétrica de um elétron seja menor do que a sua carga real. Imagine, neste contexto, duas cargas elétricas colocadas a uma distância de tal forma a medir a força entre elas. Um experimento simples de balança eletrostática. Dependendo da distância entre as duas cargas, grande parte das cargas elétricas das partículas estarão mascaradas (screening) por este efeito de polarização. Na medida em que aproximamos as cargas, elas penetram cada vez mais na nuvem polarizada da outra, diminuindo o efeito de screening e, consequentemente, observa-se um valor de carga elétrica maior. Como resultado, a medida da carga elétrica de um elétron depende da distância na qual ela foi medida. O valor que adotamos, na prática, $\alpha = 1/137$ é um valor assintótico deste efeito. Para se ter uma ideia, na escala de energia típica da massa do bóson Z (~ 90 GeV), temos que $\alpha^{90\text{ GeV}} \sim 1/127$ .nn
n
nn

nFigura 8 – Esquema de um elétron livre.
n
nnnn

nFigura 9 – Polariazação do vácuo por conta de um elétron.
n
nnnnNas interações fortes, cuja teoria para descrevê-las é a Cromodinâmica Quântica (QCD, em Inglês), os glúons são os bósons mediadores. Ao invés da carga elétrica, as interações surgem em partículas que possuam cargas de cor, que são três (red, green e blue), com suas respectivas anti-cores (anti-red, anti-green e anti-blue). Note que na QED há apenas uma carga (e sua respectiva anti-carga). O diagrama básico de interação é o mostrado na figura 10.n
n
nn

nFigura 10 – Bloco básico para construção de diagramas na QCD.
n
nnAo contrário da QED, onde uma partícula carrega apenas uma carga elétrica (e a anti-partícula, sua anti-carga), um quark pode carregar três valores diferentes de carga de cor. Portanto, é possível, em uma interação, a mudança de carga de cor de um quark. Como deve haver conservação da carga de cor, isto só é possível se o glúon também possuir carga de cor. Assim, um quark carregando carga vermelha, para se tornar verde, deve interagir com um glúon que tenha uma componente verde + anti-vermelha. Pelo fato de haver três cargas de cor, podemos fazer no máximo 3×3=9 combinações de cor+anticor responsáveis por estas interações. Contudo, há apenas oito glúons. Para entender isso, vamos representar um estado de cor como sendo um vetor de três dimensões e, neste caso, um glúon seria representado por uma matrix de 3×3 posições, de modo que um estado de cor se transformaria em outro estado através de:nn
n n n n n n

$\begin{pmatrix}rnr$

n nnEstados de anti-cor poderiam ser representados por:nn
n n n n n n

$\begin{pmatrix}rn\bar r$

n nnNesta representação podemos interpretar que as colunas na matriz do glúon representam as três anti-cores enquanto as linhas representam as três possíveis cores. Assim, um glúon pode ser compreendido como um bóson em eu estado de cor + anti-cor. Por exemplo, um glúon pode possuir uma carga de cor vermelho + anti-verde, por exemplo, no qual poderíamos representar como $|\text{gluon}}\rangle = |r\bar g\rangle$ . Neste caso, poderíamos fazer 9 possíveis combinações de cor + anti-cor, totalizando 9 possíveis tipos de glúons. Um destes possíveis glúons, dado por $|\text{gluon}\rangle =\tfrac{1}{\sqrt{3}} (|r \bar r\rangle + |g \bar g\rangle + |b \bar b\rangle)$ é totalmente neutro em cor e, no final das contas, não acarreta em nenhum efeito perceptível de interação. Além disso, por ser uma partícula totalmente neutra de cor deveria ser observado experimentalmente, o que não é o caso. Por conta disso, são 8 os possíveis glúons existentes. Há argumentos de que este nono glúon seria o fóton, o que seria interessante em um esquema de unificação. Contudo, se o fóton fosse um glúon ele deveria acoplar com partículas sem cargas elétricas, o que não é o caso. Os 8 glúons restantes, por razões que discutiremos mais a frente na disciplina, são representados por elementos do grupo SU(3), que possuem 8 geradores independentes, representados por matrizes de 3×3 dimensões. Uma das representações das matrizes do grupo SU(3) pode ser observada neste link. Neste caso, os 8 glúons seriam dados por:nn
n n n n n n

$\begin{matrix}rn(r\bar{b}+b\bar{r})/\sqrt{2} \\rn-i(r\bar{b}-b\bar{r})/\sqrt{2} \\rn(r\bar{g}+g\bar{r})/\sqrt{2}\\rn-i(r\bar{g}-g\bar{r})/\sqrt{2}\\rn(b\bar{g}+g\bar{b})/\sqrt{2}\\rn-i(b\bar{g}-g\bar{b})/\sqrt{2}\\rn(r\bar{r}-b\bar{b})/\sqrt{2}\\rn(r\bar{r}+b\bar{b}-2g\bar{g})/\sqrt{6}\\rn\end{matrix}$

n nnO interessante desta formulação é que, além destes 8 glúons serem totalmente independentes, isto é, é impossível combinar quaisquer dois ou mais glúons para formar um terceiro, diferente, é impossível combinar quaisquer destes glúons para formar um estado totalmente neutro de cor, corroborando com a não observação do glúon neutro de cor. A escolha de outras bases tornaria isto possível. 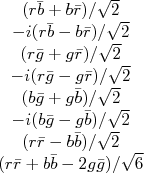O interessante da QCD, que a torna particularmente rica, é a possíbilidade, por conta de glúons possuirem cargas de cor, que eles interajam fortemente entre sí, ou seja, os diagramas mostrados na figura 11 são possíveis em QCD.n
n
nn

nFigura 11 – Interações entre glúons na QCD.nn
n
nDa mesma forma que para uma carga eletrica, uma carga de cor tem uma estrutura complexa. Se não houvesse a possibilidade de interação entre glúons, uma carga de cor, por exemplo em um quark, teria o mesmo comportamento de uma carga elétrica e o efeito de polarização do vácuo seria idêntico. Porém, por conta da possibilidade de vértices de três ou quatro glúons, como mostrados na figura 11, uma carga de cor tem uma estrutura um pouco diferente, como esquematizado na figura 12. Como glúons carregam cor, uma carga de cor tem uma preferência por ficar rodeada por cargas similares, ao contrário da carga elétrica, onde uma carga tem preferência por ficar rodeada por cargas opostas. Neste caso, ao se aproximar de uma carga de cor, você penetra em uma nuvem de polarização inversa ao observado no caso elétrico e, neste caso, a carga observada diminui. É um efeito totalmente oposto ao eletromagnético. Neste caso, a longas distâncias, observa-se uma carga de cor muito maior que em curtas distâncias. A consequência disto é que a interação entre cargas de cor diminui com a distância. Este efeito é conhecido como liberdade assintótica na QCD. n
n
nn

nFigura 12 – Estrutura de uma carga de cor.
n
n

nFigura 13 – Acoplamento em função da distância para a QED e para a QCD.n
n
nnNa figura 13 mostramos como a constante de acoplamento na QED e QCD dependem da distância (neste caso, momento transferido, que está relacionado à distância). Note como o comportamento para QED é diferente da QCD. Isto por conta dos possíveis acoplamentos entre glúons. Além de consequências fenomenológicas importantes, esta diferença tem implicações práticas. Diagramas de Feynman pressupõe um cálculo perturbativo, onde o acoplamento é fraco. No caso da QED, as distâncias onde a constante de acoplamento são grandes são muito pequenas que, em situações práticas, não ocorrem. Por conta disso o cálculo de diagramas de Feynman funcionam muito bem em QED. No caso da QCD, porém, a constante de acoplamento é grande e diminui com a distância. Neste caso, cálculos perturbativos somente são confiáveis em processos com grande transferência de momento, onde distâncias muito curtas estão envolvidas.n
n
nnInterações eletromagnéticas e fortes diferem também pela sua intensidade. Tome por exemplo, o esquema do decaimento eletromagnético do píon, na figura 7. Compare, por exemplo, ao diagrama do decaimento da partícula $\Delta^{++} \rightarrow p+\pi^+$ , na figura 14. Em ambos os casos o diagrama mostrado é de primeira ordem, e, por conta disto, a taxa de transição é proporcional ao quadrado do potencial perturbativo. Porém, no primeiro caso, há uma interação eletromagnética e no segundo, uma interação forte. Uma estimativa simples, levando em consideração que o alcance da interação forte é da ordem de 1 fm, sugere que a vida média do $\Delta^{++}$ seja da ordem de $\tau \sim 1\text{ fm}/c \sim 10^{-23}\text{ s}$ . 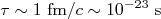De fato, esta é a ordem de grandeza da vida média desta partícula para este decaimento. No caso do píon neutro, mede-se que sua vida média é da ordem de 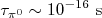$\tau_{\pi^0} \sim 10^{-16}\text{ s}$ . Se caracterizarmos a intensidade do potencial de interação por uma constante de acoplamento, normalmente chamada de $\alpha$ , teríamos que:nn
n n n n n n

$\frac{\tau_{em}}{\tau_s} \sim \left(\frac{\alpha_{em}}{\alpha_s} \right)^2 \sim 10^{-5} - 10^{-7} \rightarrow \frac{\alpha_{em}}{\alpha_s} \sim 10^{-3}$

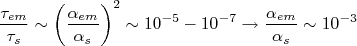n nnque mostra que a interação eletromagnética é cerca de 3-4 ordens de grandeza menos intensa que a interação forte. Se não fosse, dificilmente conseguiríamos fazer um estado ligado com cargas positivas, como o próton e demais núcleos atômicos.n
n
nn

nFigura 14 – Decaimento do $\Delta^{++} \rightarrow p+\pi^+$ .nn
n
nContudo, são observados decaimentos com vida média muito mais longa que as típicas das interações eletromagnéticas, por exemplo, o decaimento do $\pi^- \rightarrow e^- +\bar{\nu}_e$ , com $\tau \sim 10^{-12}\text{ s}$ , o $\Sigma^+ \rightarrow n + \pi^+$ , com $\tau \sim 10^{-10}\text{ s}$ ou até mesmo o decaimento do nêutron $n \rightarrow p + e^- +\bar{\nu}_e$ , com vida média de 15 minutos e muitas outras partículas. Estas vidas médias muito longas sugerem interações muito mais fracas que a eletromagnética, da ordem de:nn
n 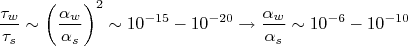n n n n n

$\frac{\tau_{w}}{\tau_s} \sim \left(\frac{\alpha_{w}}{\alpha_s} \right)^2 \sim 10^{-15} - 10^{-20} \rightarrow \frac{\alpha_{w}}{\alpha_s} \sim 10^{-6} - 10^{-10}$

n nnO interessante desta interação fraca é que o bóson responsável por ela se acopla tanto a quarks quanto a léptons. Mais interessante ainda, olhando o decaimento do nêutron, esquematizado na figura 15, é o fato de esta interação alterar o sabor dos quarks. Neste caso, um quark d torna-se um quark u, o que não é observado na interação eletromagnética e forte.
n
nn

nFigura 15 – Decaimento do nêutron.
n
n

nFigura 16 – Decaimento do múon.
n
nnnPoderíamos tratar a interação fraca como algo novo, independente das demais interações. Por outro lado, percebe-se que as interações fracas são muito similares às eletromagnéticas, podendo serem tratadas como tal, com a diferença de o mediador serem bósons extremamente massivos, de modo a diminuir a intensidade do acoplamento. Para explicar estas intensidades, são necessários bósons com massa da ordem de 100 vezes a massa do próton. A consequência de necessitarmos de bósons tão massivos é o curtíssimo alcance da interação fraca, da ordem de 10^-3 fm. São necessários três bósons massivos para explicar as interações fracas. Um deles é neutro (Z) e os outros dois, carregados (W^– e W⁺).n
n
nNa figura 17 mostramos alguns vértices de interação com o bóson Z e W^–. Note que, por conta do W ser carregado, ele altera o estado do lépton e do quark, de modo a conservar a carga elétrica. No caso do quark, esta mudança acaba alterando o sabor do quark. No exemplo, o quark d torna-se u. n
n
nn

nFigura 17 – Alguns vértices para a interação fraca.
n
n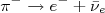nnDevemos lembrar, contudo, que o acoplamento destes bósons em vértices envolvendo léptons ocorre dentro da mesma geração destas partículas, de modo a conservar os números quânticos leptônicos individualmente. Neste caso, um elétron não acopla com um neutrino do tau, e assim por diante. A partir de diagramas deste tipo é possível representar diversos decaimentos fracos. Por exemplo, o decaimento $\pi^- \rightarrow e^- + \bar\nu_e$ pode ser representado pelo esquema mostrado na figura 18.n
n
nn

nFigura 18 – Decaimento do píon negativo.
n
nnnUma consequência importante da interação fraca é que bósons W e Z se acoplam em vértices de 3 ou 4 bósons, assim como no caso dos glúons e, no caso de bósons W, por possuirem carga elétrica, também se acoplam a fótons. Estes acoplamentos são mostrados na figura 19.n
n
nn

nFigura 19 – Acoplamentos entre bósons Z e W e fóton.n
n
nnn

Leitura recomendada

Capítulo 2 do livro “Introduction to Elementary Particles”, David Griffths.n
Capítulo 2 do livro “Quarks & Leptons”, Francis Halzen e Alan D. Martinn

n
n

Exercícios

]]>

Diagramas de Feynman e uma discussão qualitativa das interações

Leitura recomendada

Exercícios

Deixe um comentário Cancelar resposta