nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
n
nnPrecisamos agora aprender a calcular os diagramas de Feynman que vimos anteriormente. Vamos nos concentrar por alguns instantes em uma única interação, representada pela troca de um fóton (ou uma outra partícula de interação). Neste caso, a transição entre os estados pode ser calculada aa partir de:nn
n
 |
n
n
n
 |
n
n
n
n

nFigura 1 – Espalhamento de uma partícula por um potencial eletromagnético.n
n
nUma partícula sem spin deve satisfazer a equação de Klein-Gordon,nn
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
 seja invariante por transformações de Lorentz. Isto é fácil de entender. A ação provocada por esta Lagrangeana em um determinado caminho deve ser invariante por transformação de Lorentz e, sendo assim:nn
seja invariante por transformações de Lorentz. Isto é fácil de entender. A ação provocada por esta Lagrangeana em um determinado caminho deve ser invariante por transformação de Lorentz e, sendo assim:nnn
 |
n
n
 somente será invariante se
somente será invariante se  for. Neste caso, devemos procurar satisfazer esta condição também para a parte referente à interação. Devemos também satisfazer a condição de que a parte de interação, no limite de baixas velocidades, se reduza à
for. Neste caso, devemos procurar satisfazer esta condição também para a parte referente à interação. Devemos também satisfazer a condição de que a parte de interação, no limite de baixas velocidades, se reduza à  , sendo
, sendo  o potencial elétrico ao qual a carga está sujeita. Sendo
o potencial elétrico ao qual a carga está sujeita. Sendo  uma das compontentes do quadrivetor potencial
uma das compontentes do quadrivetor potencial  , é fácil ver que a Lagrangeana de interação deve incluir algum tipo de produto entre quadrivetores, sendo um deles o quadrivetor potencial. Deve ser também proporcional à carga elétrica e inversamente proporcional à
, é fácil ver que a Lagrangeana de interação deve incluir algum tipo de produto entre quadrivetores, sendo um deles o quadrivetor potencial. Deve ser também proporcional à carga elétrica e inversamente proporcional à  , como a Lagrangeana livre, de modo a manter
, como a Lagrangeana livre, de modo a manter  invariante. É fácil ver que:nn
invariante. É fácil ver que:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
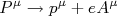 |
n
n
 . Substituindo na Eq. de Klein-Gordon, temos:nn
. Substituindo na Eq. de Klein-Gordon, temos:nnn
 |
n
n
n
 |
n
n
 . Sabendo que a carga do elétron vale
. Sabendo que a carga do elétron vale  , com
, com  podemos, em uma teoria de perturbação de primeira ordem, tomar que o potencial perturbativo é apenas
podemos, em uma teoria de perturbação de primeira ordem, tomar que o potencial perturbativo é apenas  nn
nnn
nnComo vimos, a amplitude de transição de um estado inicial, i, para um estado final, f, é escrita como:nn
n
 |
n
n
n
 |
n
n
n
 |
n
n
 , pode ser resolvido por partes, através da relação
, pode ser resolvido por partes, através da relação  , que é particularmente útil por permitir que eu transfira as derivadas para o estado final. Deste modo:nn
, que é particularmente útil por permitir que eu transfira as derivadas para o estado final. Deste modo:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
 é a corrente de partículas do estado inicial para o final nesta transição. Tomando que as partículas inicial e final são partículas livres, isto é,
é a corrente de partículas do estado inicial para o final nesta transição. Tomando que as partículas inicial e final são partículas livres, isto é,  , com
, com  o quadrimomento inicial e/ou final da partícula,
o quadrimomento inicial e/ou final da partícula,  , uma constante de normalização, pode-se calcular a corrente de partículas como sendo:nn
, uma constante de normalização, pode-se calcular a corrente de partículas como sendo:nnn
 |
n
n
 de modo a calcular a amplitude de transição do estado inicial para o final. Acontece que o diagrama mostrado na figura 1 é apenas um pedaço do processo. De onde veio o fóton? Podemos, por exemplo, considerar que o fóton é devido à interação eletromagnética entre o elétron e uma outra partícula. Vamos tomar esta outra partícula como sendo um múon, de modo a evitar complicações, por enquanto, por conta de partículas idênticas. Neste caso, temos um diagrama como o representado na figura 2.
de modo a calcular a amplitude de transição do estado inicial para o final. Acontece que o diagrama mostrado na figura 1 é apenas um pedaço do processo. De onde veio o fóton? Podemos, por exemplo, considerar que o fóton é devido à interação eletromagnética entre o elétron e uma outra partícula. Vamos tomar esta outra partícula como sendo um múon, de modo a evitar complicações, por enquanto, por conta de partículas idênticas. Neste caso, temos um diagrama como o representado na figura 2.n
n

nFigura 2 – Espalhamento elétron múon.
n
n
n
 |
n
n
 . Como
. Como  é uma exponencial simples, é fácil integrar esta equação e, por conta disso, escrevemos que:nn
é uma exponencial simples, é fácil integrar esta equação e, por conta disso, escrevemos que:nnn
 |
n
n
 , o momento transferido na interação. Substituindo (23) em (19), lembrando de adaptar os índices para a corrente do elétron, temos que:nn
, o momento transferido na interação. Substituindo (23) em (19), lembrando de adaptar os índices para a corrente do elétron, temos que:nnn
 |
n
n
n
![T_{if} = -i N_A N_B N_C N_D \left[ \frac{1}{i^3} (-ie)(p_A+p_C)^\mu \left( -i\frac{g_{\mu\nu}}{q^2}\right) (-ie)(p_B+p_D)^\nu \right] \int{e^{-i(p_C+p_D - p_A - p_B)^\mu x_\mu}d^4x} T_{if} = -i N_A N_B N_C N_D \left[ \frac{1}{i^3} (-ie)(p_A+p_C)^\mu \left( -i\frac{g_{\mu\nu}}{q^2}\right) (-ie)(p_B+p_D)^\nu \right] \int{e^{-i(p_C+p_D - p_A - p_B)^\mu x_\mu}d^4x}](http://picard.if.usp.br/sampa/blog/pivotx/extensions/renderlatex/pictures/a9f42404b5a5b8b04257cc41b2b2b4d2.png) |
n
n
n
 |
n
n
n
 |
n
n
n
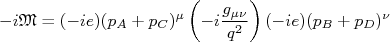 |
n
n
 , referente ao fóton que é transmitido de uma partícula para a outra. Este termo é denominado propagador. O quadrimomento do fóton,
, referente ao fóton que é transmitido de uma partícula para a outra. Este termo é denominado propagador. O quadrimomento do fóton,  é determinado pela conservação do quadrimomento total. O processo como todo tem intensidade proporcional à carga do elétron ao quadrado (que é a mesma carga do múon), ou seja, é proporcional à constante de estrutura fina
é determinado pela conservação do quadrimomento total. O processo como todo tem intensidade proporcional à carga do elétron ao quadrado (que é a mesma carga do múon), ou seja, é proporcional à constante de estrutura fina  . Neste caso, podemos dizer que cada vértice contribui com uma intensidade, na transição, de
. Neste caso, podemos dizer que cada vértice contribui com uma intensidade, na transição, de  e, pelo processo como um todo ser proporcional à
e, pelo processo como um todo ser proporcional à  dizemos que este é um diagrama de primeira ordem.n
dizemos que este é um diagrama de primeira ordem.nn
n

nFigura 3 – Identificação dos termos do elemento de matriz no diagrama de Feynman.n
n
nNote que calculamos, essencialmente a amplitude de transição de um estado para outro. A probabilidade de transição é essencialmente
 . Da mesma forma, definimos que a taxa de transição por unidade de volume domo sendo
. Da mesma forma, definimos que a taxa de transição por unidade de volume domo sendo  . Acontece que não se mede taxas de transição. O que se mede são seções de choque ou vidas médias de decaimento. Seção de choque para um determinado processo é definida como:nn
. Acontece que não se mede taxas de transição. O que se mede são seções de choque ou vidas médias de decaimento. Seção de choque para um determinado processo é definida como:nnn
 |
n
n
 é o fluxo de partículas incidente (também chamada luminosidade) e
é o fluxo de partículas incidente (também chamada luminosidade) e  é o número de partículas observadas por unidade de tempo no detector. Podemos relacionar a expressão acima com a taxa de transição através de:nn
é o número de partículas observadas por unidade de tempo no detector. Podemos relacionar a expressão acima com a taxa de transição através de:nnn
 |
n
n
 , observado que os estados devem ser normalizados no volume que estamos calculando, ou seja,
, observado que os estados devem ser normalizados no volume que estamos calculando, ou seja,  . Deste modo:nn
. Deste modo:nnn
 |
n
n
 aparece quadraticamente, temos duas destas integrais. Uma delas vai resultar em
aparece quadraticamente, temos duas destas integrais. Uma delas vai resultar em  . A outra pode ser trabalhada, resultando em
. A outra pode ser trabalhada, resultando em  , que cancela com um desses termos. Deste modo:nn
, que cancela com um desses termos. Deste modo:nnn
 |
n
n
 , isto é,
, isto é,  . Em uma das direções, a função de onda da partícula pode ser descrita como
. Em uma das direções, a função de onda da partícula pode ser descrita como  , sendo nula em
, sendo nula em  e
e  . Neste caso,
. Neste caso,  , com
, com 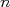 inteiro. Ou seja, os momentos são discretos com separação entre eles dada por
inteiro. Ou seja, os momentos são discretos com separação entre eles dada por  . Em um intervalo
. Em um intervalo  , cabem então
, cabem então  partículas. Sendo assim, considerando uma caixa cúbica, o número de partículas que cabem em um determinado volume para um intervalo de momento pode ser dado por:nn
partículas. Sendo assim, considerando uma caixa cúbica, o número de partículas que cabem em um determinado volume para um intervalo de momento pode ser dado por:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
 |
n
n
 enquanto o número de partículas por volume de B é
enquanto o número de partículas por volume de B é  . Deste modo, podemos escrever que:nn
. Deste modo, podemos escrever que:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
 como sendo um número que estabelece o tamanho do espaço de fase, e vale:nn
como sendo um número que estabelece o tamanho do espaço de fase, e vale:nnn
 |
n
n
 quando
quando  são fatores geométricos para estabelecer a grandeza medida. Toda a física está contida na amplitude de transição
são fatores geométricos para estabelecer a grandeza medida. Toda a física está contida na amplitude de transição  .n
.nn
Leitura recomendada
n- n
- Capítulo 4 do livro “Quarks & Leptons”, Francis Halzem e Alan Martin.n
- Capítulo 6 do livro “Introduction to Elementary Particles”, D. Griffths.n
Exercícios
n- n
- Mostre que no centro de massas para uma reação
 n
n n
n nonde
nonde  é o elemento de ângulo sólido,
é o elemento de ângulo sólido,  e
e  no centro de massa.n
no centro de massa.n
- No espalhamento elétron – elétron há dois diagramas de Feynman que contribuem para o processo em primeira ordem, já que não conseguimos distinguir as partículas C e D. Desenhe estes diagramas e calcule
 como sendo a soma das amplitudes para cada diagrama. Mostre que podemos escrever que:
como sendo a soma das amplitudes para cada diagrama. Mostre que podemos escrever que:
n
n n
n
n
n - Repita o exercício anterior para o caso do espalhamento elétron-pósitron. Neste caso há também dois diagramas, um de espalhamento e outro de aniquilação e posterior conversão do fóton de aniquilamento em um par elétron pósitron. Para o pósitron, considere-o como uma partícula viajando ao passado e, neste caso, o quadrivetor momento tem sinal invertido ao que fizemos nesta aula. Mostre que:
n
n n
n
n
n - Define-se a largura de decaimento
 como sendo a probabilidade por unidade de tempo de uma partícula desintegrar, ou seja
como sendo a probabilidade por unidade de tempo de uma partícula desintegrar, ou seja  onde
onde  é o número de partículas em uma amostra. Seguindo argumentos muito similares ao que deduzimos para a sessão de choque, mostre que, em um decaimento
é o número de partículas em uma amostra. Seguindo argumentos muito similares ao que deduzimos para a sessão de choque, mostre que, em um decaimento  que:
que:
n
n nn
nn
- Em um decaimento de dois corpos,
 , mostre que integrando sobre todas as direções de momento das partículas 1 e 2 no centro de massa da partícula A que:
, mostre que integrando sobre todas as direções de momento das partículas 1 e 2 no centro de massa da partícula A que:
n
n n
n
Deixe um comentário