nnVersão para impressãon nn Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.n nn O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina. n
nnNo cálculo de um diagrama de Feynman temos que considerar dois aspectos importantes: primeiramente o espaço de fase envolvido, tanto inicial quanto final. Estes são importantes nos cálculos se seções de choque e de taxas de decaimento, por exemplo. Contudo, são aspectos quase que geométricos e de contabilidade. Um segundo aspecto é o cálculo do elemento de matrix
 , que contém as informações sobre os processos físicos, e é obtido a partir do conhecimento do tipo de interação envolvida no diagrama. Para um caso simples, de uma interaçào eletromagnética que não envolve spin das partículas, nós obtivemos, por exemplo, que:nn
, que contém as informações sobre os processos físicos, e é obtido a partir do conhecimento do tipo de interação envolvida no diagrama. Para um caso simples, de uma interaçào eletromagnética que não envolve spin das partículas, nós obtivemos, por exemplo, que:nnn
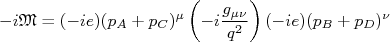 |
n
n
n
nPodemos escrever que a equação de Dirac para uma partícula livre é dada pornn
n
 |
n
n
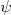 tem a forma:nn
tem a forma:nnn
 |
n
n
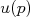 é um vetor de quatro dimensões. Nós já discutimos que, a presença de uma interação eletromagnética é obtida por uma substituição do tipo
é um vetor de quatro dimensões. Nós já discutimos que, a presença de uma interação eletromagnética é obtida por uma substituição do tipo 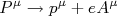 . Neste caso, podemos reescrever a equação de Dirac como sendo:nn
. Neste caso, podemos reescrever a equação de Dirac como sendo:nnn
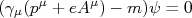 |
n
n
n
 |
n
n
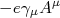 , que podemos utilizar para calcular a amplitude da transição do estado inicial para o final.nn
, que podemos utilizar para calcular a amplitude da transição do estado inicial para o final.nnn
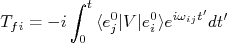 |
n
n
n
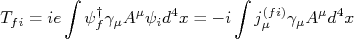 |
n
n
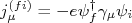 , a densidade de corrente. Se tomarmos a equação (3) para descrever os estados inicial e final da partícula sujeita à ação do campo eletromagnético, podemos escrever que:nn
, a densidade de corrente. Se tomarmos a equação (3) para descrever os estados inicial e final da partícula sujeita à ação do campo eletromagnético, podemos escrever que:nnn
 |
n
n
 . Se nós seguirmos os mesmos raciocínios utilizados anteriormente, nós podemos escrever que o elemento de matriz para um espalhamento de primeira ordem entre duas partículas é dado por:nn
. Se nós seguirmos os mesmos raciocínios utilizados anteriormente, nós podemos escrever que o elemento de matriz para um espalhamento de primeira ordem entre duas partículas é dado por:nnn
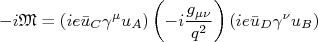 |
n
n
n
 |
n
n
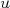 para partículas incidentes e
para partículas incidentes e  para partículas emergentes. Há uma diferença no fator de acoplamento nos vértices que, no caso com spin, é dado por uma matriz que acopla o estado inicial ao final. Os propagadores, nestes casos, são idênticos, uma vez que eles surgem da resolução da eq. de Maxwell
para partículas emergentes. Há uma diferença no fator de acoplamento nos vértices que, no caso com spin, é dado por uma matriz que acopla o estado inicial ao final. Os propagadores, nestes casos, são idênticos, uma vez que eles surgem da resolução da eq. de Maxwell  .n
.nn
n

nFigura 1 – Representação do elemento de matriz de transição nos diagramas de Feynman para sistemas sem e com spin.n
n
nnPode-se ver que parece haver uma estrutura “gráfica” para a construção de elementos de matriz para interações através de diagramas de Feynman. Contudo, nos restringimos, até o momento, a léptons como partículas externas e a fótons como propagadores. Há muito mais opções para partículas mensuráveis, além de léptons, e para propagadores. Vamos, inicialmente, discutir o caso de um fóton, seja como partícula incidente ou emergente da interação e, em seguida, discutiremos alguns aspectos acerca de propagadores.n
n
nA função de onda para um fóton satisfaz a equação:nn
n
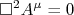 |
n
n
n
 |
n
n
 , o que só é verdade no caso da massa do fóton ser nula. O quadrivetor
, o que só é verdade no caso da massa do fóton ser nula. O quadrivetor  , que depende do momento do fóton
, que depende do momento do fóton  é chamado de polarização do fóton. Sabemos de eletrodinâmica que o fóton possui dois estados de polarização e elas devem ser transversais ao momento do fóton (lembre-se que o campo elétrico e magnético são transversais à direção de propagação da onda eletromagnética) mas o quadrivetor polarização possui quatro componentes. Contudo, duas destas componentes podem ser escolhidas arbitrariamente devido à vínculos impostos no eletromagnetismo. Por exemplo, utilizando a condição de que
é chamado de polarização do fóton. Sabemos de eletrodinâmica que o fóton possui dois estados de polarização e elas devem ser transversais ao momento do fóton (lembre-se que o campo elétrico e magnético são transversais à direção de propagação da onda eletromagnética) mas o quadrivetor polarização possui quatro componentes. Contudo, duas destas componentes podem ser escolhidas arbitrariamente devido à vínculos impostos no eletromagnetismo. Por exemplo, utilizando a condição de que  , escolhendo o eixo-z como a direção do vetor momento do fóton, podemos automaticamente dizer que a terceira componente do vetor polarização do fóton deve ser nula para satisfazer esta condição. Além desta condição, o calibre de Lorentz do potencial vetor que faz com que:nn
, escolhendo o eixo-z como a direção do vetor momento do fóton, podemos automaticamente dizer que a terceira componente do vetor polarização do fóton deve ser nula para satisfazer esta condição. Além desta condição, o calibre de Lorentz do potencial vetor que faz com que:nnn
 |
n
n
n
 |
n
n
 , só é verdadeira se a componente temporal do quadrivetor polarização do fóton for nula. Neste caso, o quadrivetor polarização é escrito como:nn
, só é verdadeira se a componente temporal do quadrivetor polarização do fóton for nula. Neste caso, o quadrivetor polarização é escrito como:nnn
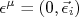 |
n
n
n
 |
n
n
 são os pesos atribuídos aos férmions externos. No caso do fóton, este peso são os quadrivetores de polarização
são os pesos atribuídos aos férmions externos. No caso do fóton, este peso são os quadrivetores de polarização  . Contudo, como já discutimos, um fóton não acopla a outro fóton. Os vértices da QED sempre envolvem um fóton com duas partículas carregadas. Para um fóton ser uma partícula externa é necessário que haja propagadores que sejam outras partículas que não o fóton. Neste caso, precisamos discutir um pouco como obter formas para outros propagadores que não sejam o fóton.n
. Contudo, como já discutimos, um fóton não acopla a outro fóton. Os vértices da QED sempre envolvem um fóton com duas partículas carregadas. Para um fóton ser uma partícula externa é necessário que haja propagadores que sejam outras partículas que não o fóton. Neste caso, precisamos discutir um pouco como obter formas para outros propagadores que não sejam o fóton.nn
nTecnicamente, propagadores correspondem à amplitude de probabilidade de uma partícula se mover de um ponto para outro com uma certa energia e momento. Neste sentido, propagadores correspondem a funções de Green para o operador que descreve a evolução da partícula. Seja, por exemplo, uma partícula sujeita a um potencial de tal forma que o seu estado possa ser descrito pela equação:nn
n
 |
n
n
n
 |
n
n
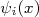 corresponde à solução da equação para a partícula livre
corresponde à solução da equação para a partícula livre  .nnA função de Green
.nnA função de Green  pode ser obtida simplesmente resolvendo a equação:nn
pode ser obtida simplesmente resolvendo a equação:nnn
 |
n
n
n
 |
n
n
n
 |
n
n
n
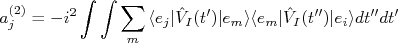 |
n
n
 . Substituindo em (22), e fazendo as integrais, é fácil obter que:nn
. Substituindo em (22), e fazendo as integrais, é fácil obter que:nnn
 |
n
n
 , que pode ser indentificado como sendo o propagador de um vértice ao outro.
, que pode ser indentificado como sendo o propagador de um vértice ao outro. 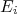 é a energia inicial, fixa. Contudo,
é a energia inicial, fixa. Contudo,  corresponde às energias dos estados intermediários e são os autovalores de nn nestes estados intermediários. Em termos de operadores, o propagador pode ser escrito justamente como mostrado em (21).
corresponde às energias dos estados intermediários e são os autovalores de nn nestes estados intermediários. Em termos de operadores, o propagador pode ser escrito justamente como mostrado em (21).n
nSendo assim, vamos calcular alguns propagadores. Para uma partícula de massa m, sem spin, a sua evolução é dada pela equação de Klein-Gordon
 , que nos faz identificar, em comparação à (17) que o propagador, neste caso é:nn
, que nos faz identificar, em comparação à (17) que o propagador, neste caso é:nnn
 |
n
n
 , o propagador é:nn
, o propagador é:nnn
 |
n
n
n
n

nFigura 2 – Resumo das regras de Feynman.n
n
nnConstruir um elemento de matriz a partir de um diagrama de Feynman pode ser feito seguindo a receita:n
n
n
- n
- Para cada linha externa associe um momento
 indicando a direção, se é uma partícula ou antipartícula.n
indicando a direção, se é uma partícula ou antipartícula.n
- Decida então, de acordo com a figura 2, a contribuição (peso) de cada uma destas linhas.n
- Para cada vértice, coloque o seu fator correspondente (ver figura 2).n
- Identifique e escreva os propagadores.n
- Para cada vértice coloque uma função delta
 n
n
- Faça a integral sobre os momentos internos dos propagadores com um fator
 .n
.n
- Reagrupe as funções delta por conta das integrações de momento.n
n
n
Leitura recomendada
n- n
- Capítulo 7 do “Introduction to elementary particles”, D. Griffths.n
- Capítulo 6 do “Quarks & Leptons”, F. Halzen e A. Martin.n
n
Exercícios
n- n
- Mostre (23)n
Deixe um comentário