Introdução

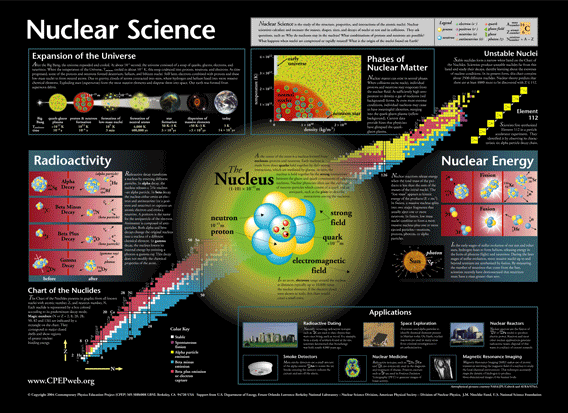
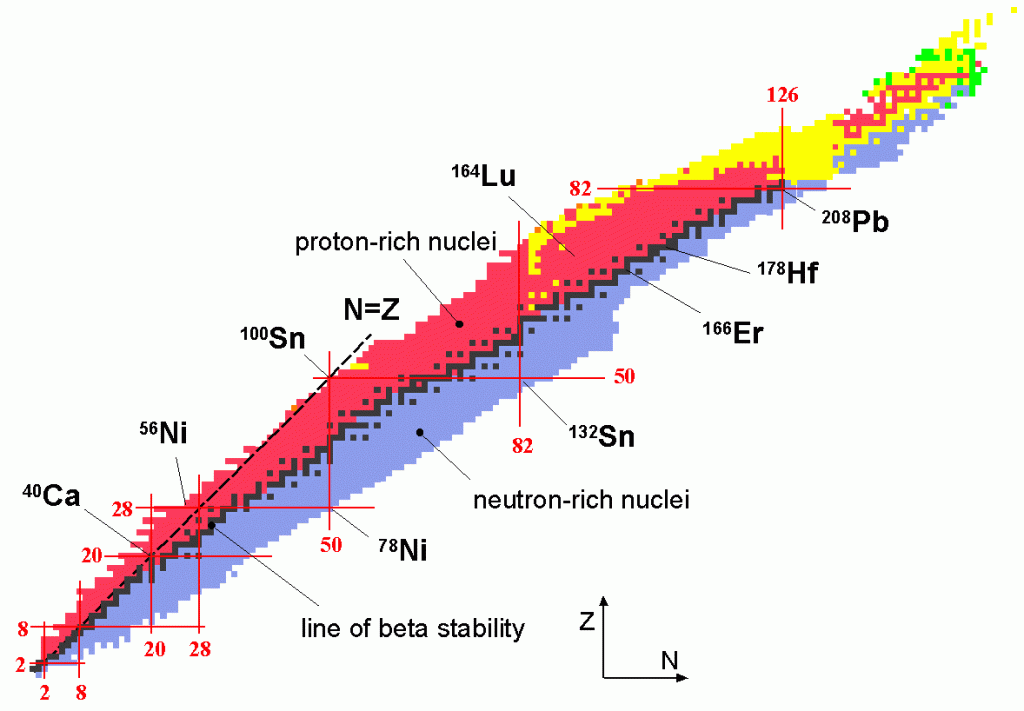
A física nuclear é uma área da física que estuda o núcleo atômico, suas propriedades físicas e como se dá a interação entre eles ou entre seus constituintes. A física nuclear atual também engloba aplicações diversas desse conhecimento em outras áreas, como energia, medicina, ciências espaciais, astrofísica, etc. A figura 1 mostra um painel sobre as características do núcleo e suas aplicações. Foi criado pela National Science Division e CPEP (the Contemporary Physics Education Project) dos EUA como uma ferramenta de educação e divulgação sobre as ciências nucleares. Essa definição, hoje em dia, principalmente para um aluno de graduação em física, parece óbvia. Nós sabemos há tempo sobre a estrutura básica da matéria, sua divisão em átomos, constituídos de um núcleo, objeto de estudo da física nuclear. Esse núcleo, por sua vez, constituído de prótons e nêutrons, que interagem através da força forte residual. Contudo, o caminho trilhado até esse nível de compreensão foi muito longo, envolvendo o esforço de muitos cientistas ao longo de décadas.

O objetivo dessa disciplina é introduzir o aluno à física nuclear. Nessa disciplina sistematizaremos o conhecimento acerca da estrutura e propriedades do núcleo atômico. Como a física nuclear é uma área na qual grande parte do desenvolvimento se deu de forma empírica, aprendendo através de experimentos, é importante, em algumas situações, contextualizar algum fenômeno sobre o ponto de vista histórico. Isso, contudo, não deve renegar o formalismo a segundo plano. É importante perceber a física nuclear como o estudo de um problema específico, um tema: o núcleo atômico. Ao contrário de outras grandes áreas da física, como o eletromagnetismo, mecânica quântica, etc. que podem ter seus conceitos aplicados em sistemas das mais diversas natureza, a física nuclear precisa ser entendida como o avesso dessa idéia. Ou seja, o sistema a ser estudado é um só. Contudo, é um sistema quântico, pelas suas dimensões e fenomenologia, e passível de interações eletromagnéticas, fraca e forte. Além de ser, quase sempre, um sistema de muitos corpos. Nesse caso, o entendimento do núcleo atômico requer o uso de ferramentas de muitas áreas da física. Nessa disciplina, em especial, usaremos vários conceitos vistos em cursos mais básicos de mecânica clássica e quântica, eletromagnetismo, física matemática e estatística.

Figura 2 – Tabela de núclídeos. Para uma versão interativa, clique aqui .

Sistemas de unidades

Pelo fato do núcleo atômico possuir dimensões muito reduzidas, o sistema de unidades que estamos habituado normalmente (SI) não é prático de ser utilizado. Vamos construir um sistema de unidades muito prático e fácil de ser utilizado em Física Nuclear. Esse sistema é baseado em um valor padrão dado pela velocidade da luz ( $c$ ). Começamos com as unidades básicas de comprimento e energia, bem como os valores no SI para velocidade da luz e constante de Planck:

$[L] = 1 \mbox{ fm} = 10^{-15} \mbox{ m}$

$1 \mbox{ MeV} = 1.6 \times 10^{-13} \mbox{ J}$

$c = 3 \times 10^{8} \mbox{ m/s} = 3 \times 10^{23} \mbox{ fm/s}$

$\hbar = 6.58 \times 10^{-22} \mbox{ MeV s}$

Com isso, podemos escrever que:

$\hbar c = 197 \mbox{ MeV fm}$

Podemos também utilizar a constante de estrutura fina, adimensional:

$\alpha = \frac{1}{137} = \frac{e^2}{\hbar c (4\pi \epsilon_0)}$

O que resulta em:

$\frac{e^2}{4\pi \epsilon_0} = 1.44 \mbox{ MeV fm}$

A unidade básica de massa pode ser obtida através da relação $E=mc^2$ , ou seja:

$[M] = \mbox{ MeV/c^2}$

da mesma forma, a unidade de tempo é definida a partir de $v=x/t$ , ou seja:

$[T] = \mbox{ fm/c}$

O uso dessas unidades são bastante convenientes. Por exemplo, qual é a velocidade de uma partícula α com energia de 4 MeV? Podemos fazer:

$E = 4 \mbox{ MeV} = \frac{1}{2} m v^2 = \frac{1}{2} 4000 \mbox{ MeV/c^2} v^2 \rightarrow v = 0.044 c$

Ou ainda, qual a energia potencial coulombiana entre uma partícula α e um núcleo de ouro a 10 fm de distância? Podemos fazer:

$E = \frac{Z_\alpha Z_{Au} e^2}{4\pi\epsilon_0 R} = 1.44 \mbox{ MeV fm} \times 2 \times 79 \times \frac{1}{10 \mbox{ fm}} = 22 \mbox{ MeV}$

Como último exemplo, qual é o comprimento de onda de de Broglie de um elétron com energia de 100 MeV? Podemos fazer:

$\lambda = \frac{h}{p} = \frac{2\pi \hbar}{p} = \frac{2\pi\hbar c}{pc}$

Sabendo que $E^2 = p^2c^2+m_e^2c^4$ e que a massa do elétron é muito menor que a energia nesse caso, temos que: $pc = E$ , e assim:

$\lambda = \frac{2\pi\hbar c}{E} = \frac{6.28 \times 197 \mbox{ MeV fm}}{100 \mbox{ MeV}} = 12 \mbox{ fm}$

Ou seja, o uso dessas unidades facilita enormemente o cálculo de valores em Física Nuclear. É muito importante, ao longo do curso, se familiarizar com esse sistema de unidades. O cálculo no SI é muito complicado e, facilmente, comentemos erros.

Leitura recomendada

The Nuclear Wall Chart (http://www.lbl.gov/abc/wallchart/guide.html)

Sistemas de unidades

Leitura recomendada

Deixe um comentário Cancelar resposta